thu gọn biểu thức A= 2x^2y+(-5x^2y)+x^2y
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


`a, A= 4xy -xy-2xy`
`= (4-1-2)xy`
`= xy`
Thay `x=2;y=3`
Ta có : `xy=2*3=6`
`b, B= x^2 y -7x^2y-4x^2y`
`=(1-7-4)x^2y`
`= -10x^2y`
Thay `x=2;y=3`
Ta có : `-10x^2y=-10*2^2 *3= -10*4*3=-40*3=-120`
`c, C=10x^2y -x^2y-7x^2y`
`=(10-1-7)x^2y`
`= 2x^2y`
Thay `x=2;y=3`
Ta có : `2x^2y=2*2^2 *3= 2*4*3=8*3=24`
`d,D=5x^2y^2-12x^2y^2+8x^2y^2`
`= (5-12+8)x^2y^2`
`=x^2y^2`
Thay `x=2;y=3`
ta có : `x^2y^2=2^2 *3^2= 4* 9=36`
 có chỗ nào bn đọc ko rõ thì ns mik nha, để mik gõ ra cho bn rõ hơn
có chỗ nào bn đọc ko rõ thì ns mik nha, để mik gõ ra cho bn rõ hơn

a: \(M=\dfrac{2}{3}\cdot\dfrac{3}{4}\cdot x^3\cdot xy^2\cdot z^2=\dfrac{1}{2}x^4y^2z^2\)
Hệ số là 1/2
Biến là \(x^4;y^2;z^2\)
b: \(N=x^2y\left(4+5-3\right)=6x^2y=6\cdot2^2\cdot\left(-1\right)=-24\)

a: Ta có: \(\left(8x^3-4x^2\right):4x-\left(4x^2-5x\right):2x+\left(2x\right)^2\)
\(=2x^2-x-2x+\dfrac{5}{2}+4x^2\)
\(=6x^2-3x+\dfrac{5}{2}\)
b: Ta có: \(\left(3x^3-x^2y\right):x^2-\left(xy^2+x^2y\right):xy+2x\left(x-1\right)\)
\(=3x-y-y-x+2x^2-2x\)
\(=2x^2-2y\)

a: Ta có: \(x^2-4x\left(3x-4\right)+7x-5\)
\(=x^2-12x^2+16x+7x-5\)
\(=-11x^2+23x-5\)
b: Ta có: \(7x\left(x^2-5\right)-3x^2y\left(xy-6y^2\right)\)
\(=7x^3-35x-3x^3y^2+18x^2y^3\)
c: Ta có: \(\left(5x+4\right)\left(2x-7\right)\)
\(=10x^2-35x+8x-28\)
\(=10x^2-27x-28\)

\(a.\) \(A=\left(15x+2y\right)-\left[\left(2x+3\right)-\left(5x+y\right)\right]\)
\(A=15x+2y-2x-3+5x+y\)
\(A=\left(15x-2x+5x\right)+\left(2y+y\right)-3\)
\(A=18x+3y-3\)
\(A=3\left(6x+y-1\right)\)
\(b.\) \(B=-\left(12x+3y\right)+\left(5x-2y\right)-\left[13x+\left(2y-5\right)\right]\)
\(B=-12x-3y+5x-2y-13x-2y+5\)
\(B=-\left(12x-5x+13x\right)-\left(3y+2y+2y\right)+5 \)
\(B=-20x-7y+5\)

\(x^2y+y^2x-2xz+2xy^2\)-\(5x^2y\)
=\(\left(x^2y-5x^2y\right)+\)\(y^2x\)-2xz+\(2xy^2\)
=-4\(x^2y\)+\(y^2x\)-2xz+\(2xy^2\)
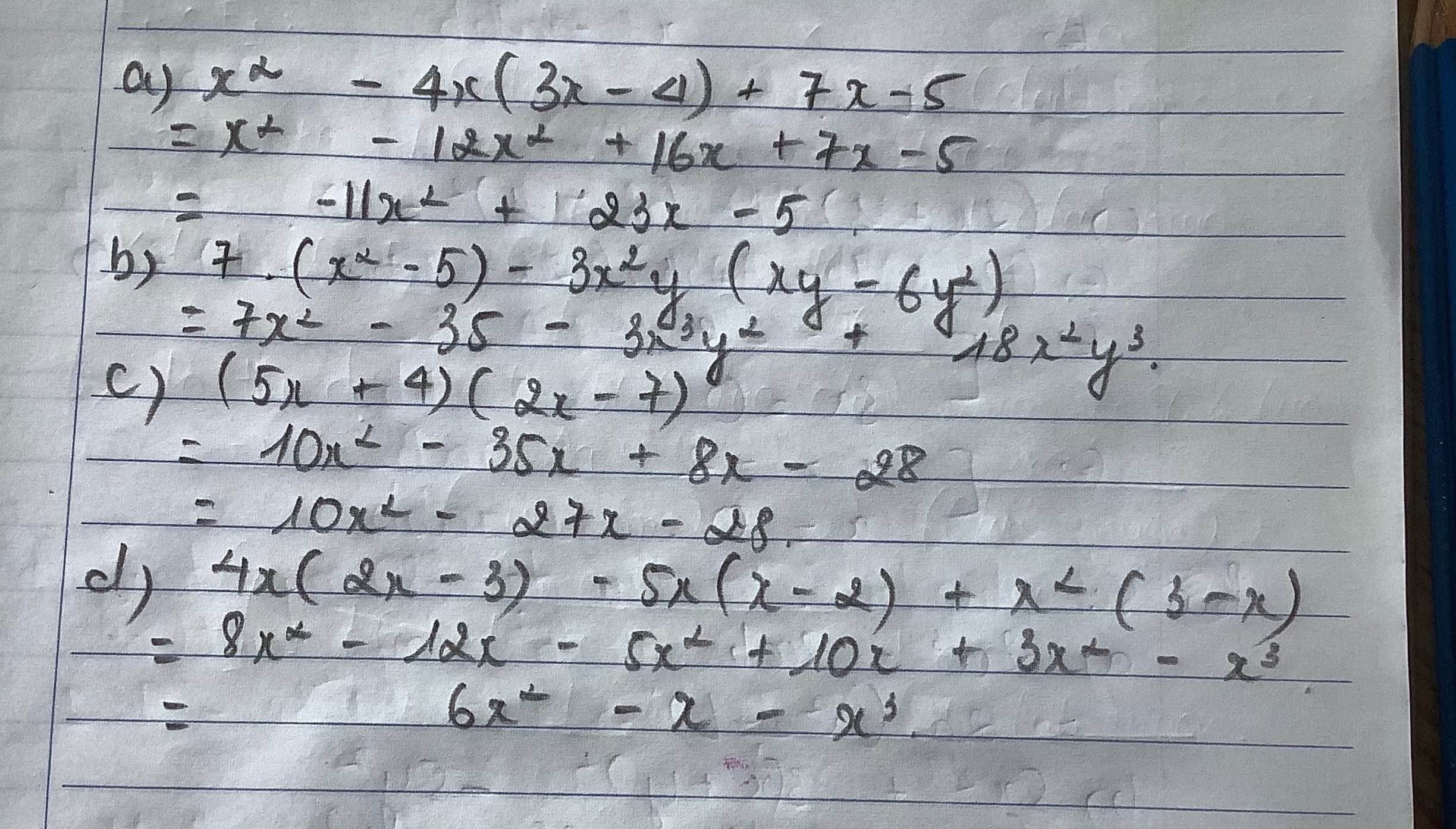
\(A=-2x^2y\)