Giúp e giải chi tiết câu 8 ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 4 2022
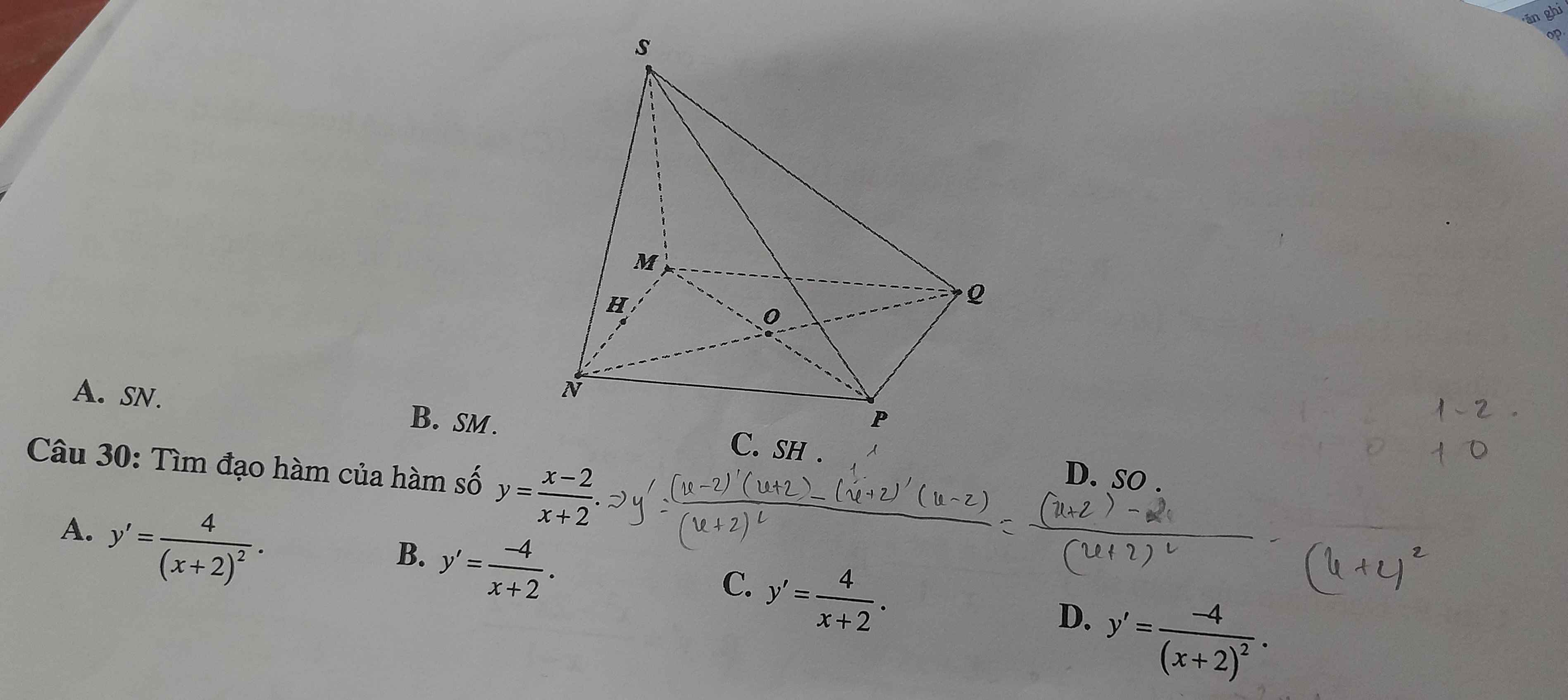
29.
SMN cân tại S \(\Rightarrow SH\perp MN\) (trung tuyến đồng thời là đường cao trong tam giác cân)
Mà \(\left\{{}\begin{matrix}MN=\left(SMN\right)\cap\left(MNPQ\right)\\\left(SMN\right)\perp\left(MNPQ\right)\end{matrix}\right.\)
\(\Rightarrow SH\perp\left(MNPQ\right)\)
Hay SH là đường cao của chóp
DT
1
29 tháng 12 2021
Câu 5:
\(\Leftrightarrow-x^2+7x-9+2x-9=0\)
\(\Leftrightarrow x^2-9x+18=0\)
=>x=3
=>Chọn A
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 3 2022
\(\lim\limits_{x\rightarrow1}f\left(x\right)=\lim\limits_{x\rightarrow1}\dfrac{mx^2-\left(m+3\right)x+3}{x-1}=\lim\limits_{x\rightarrow1}\dfrac{\left(x-1\right)\left(mx-3\right)}{x-1}\)
\(=\lim\limits_{x\rightarrow1}\left(mx-3\right)=m-3\)
\(f\left(1\right)=m^2-15\)
Hàm liên tục tại \(x=1\) khi:
\(m-3=m^2-15\Rightarrow m^2-m-12=0\Rightarrow\left[{}\begin{matrix}m=4\\m=-3\end{matrix}\right.\)
\(4^2+\left(-3\right)^2=25\)
18 tháng 5 2022
\(\begin{array} {l} 13)\\ n_{HCHO}=\dfrac{1,2}{30}=0,04(mol)\\ HCHO\xrightarrow{+AgNO_3/NH_3,t^o}4Ag\\ n_{Ag}=4n_{HCHO}=0,16(mol)\\ m=0,16.108=17,28(g)\\ \to A\\ 14)\\ X:C_nH_{2n}\\ n_{Br_2}=\dfrac{8}{160}=0,05(mol)\\ C_nH_{2n}+Br_2\to C_nH_{2n}Br_2\\ n_{C_nH_{2n}}=n_{Br_2}=0,05(mol)\\ M_{C_nH_{2n}}=14n=\dfrac{1,4}{0,05}=28(g/mol)\\ n=2\\ X:C_2H_4\\ \to A \end{array}\)
AM
15 tháng 5 2022
Hi bạn, câu 29 này mình có cái cách này dùng cho các bài lim khi rơi vào trường hợp vô định thì bạn dùng quy tắc L'Hospital làm cho nhanh với trường hợp các bài trắc nghiệm như thế này
Ở bài 29 này đang rơi vào dạng \(\dfrac{0}{0}\) nên dùng quy tắc L'Hospital được nè. Bạn làm như sau:
ĐKXĐ: \(\left\{{}\begin{matrix}x\ne1\\x\ge-3\end{matrix}\right.\)
Bước 1: Đạo hàm tử mẫu, ta được: \(\dfrac{\dfrac{1}{2}\left(x+3\right)^{-\dfrac{1}{2}}}{1}\)
Bước 2: Thay điểm cần tính giới hạn: (x=1)
ta sẽ được \(\dfrac{1}{4}\)
Vậy \(lim_{x\rightarrow1}\dfrac{\sqrt{x+3}-2}{x-1}=\dfrac{1}{4}\)
\(\Rightarrow a=1;b=4\)
Vậy S=4a-b=0
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 4 2022
\(y'=3x^2-2\)
hệ số góc tiếp tuyến tại điểm có hoành độ \(x_0=-1\) là \(y'\left(-1\right)\)
\(y'\left(-1\right)=3.\left(-1\right)^2-2=1\)
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 12 2022
ĐKXĐ: \(x>0\)
\(log_2\left(x^2+4\right)-log_2x-3=0\)
\(\Leftrightarrow log_2\left(x^2+4\right)=log_2x+3\)
\(\Leftrightarrow log_2\left(x^2+4\right)=log_2\left(9x\right)\)
\(\Leftrightarrow x^2+4=9x\)
\(\Leftrightarrow x^2-9x+4=0\)
\(\Rightarrow x_1+x_2=9\) theo định lý Viet
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 4 2022
14.
A là khẳng định sai, CD không vuông góc SB
(Vì nếu \(CD\perp SB\) (1); do \(SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\) (2)
(1);(2) \(\Rightarrow CD\perp\left(SAB\right)\Rightarrow CD\perp AB\) (vô lý do \(CD||AB\))
\(y'=\left(x^3\right)'-\left(3x\right)'+\left(4\right)'=3x^2-3\)
Hệ số góc tiếp tuyến tại điểm có hoành độ -2 là \(y'\left(-2\right)\)
\(y'\left(-2\right)=3.\left(-2\right)^2-3=9\)