Tập hợp các giá trị của x thỏa mãn |x2-5| +| 5-x2| = 40
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


4:
\(P=\left(x+4\right)\left(x^2-4x+16\right)-\left(64-x^3\right)\)
\(=x^3+64-64+x^3=2x^3\)
Khi x=-20 thì \(P=2\cdot\left(-20\right)^3=-16000\)
=>Chọn C
2: Đề khó hiểu quá bạn ơi

Vì Ix^2-5I=I5-x^2I nên:
(x^2-5)+(5-x^2)=20+20
=> x^2-5=20
=> x^2=25
=> x=5

Chọn C.
+) Ta có ![]()
![]()
+) Theo giả thiết hàm số đạt cực trị tại ⇔ phương trình (1) có 2 nghiệm phân biệt
![]()
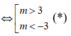
+) Với điều kiện (*) thì phương trình (1) có nghiệm x 1 , x 2 , theo Vi-ét ta có:
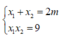
+) Ta lại có ![]()
![]()
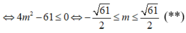
+) Kết hợp (*), (**) và điều kiện m dương ta được: 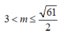


Đáp án: x=-1 Giải thích các bước giải:
x(x-5)(x+5)-(x+2)( x 2 -2x+4 )=17
⇔x( x 2 +5x-5x-25)-( x 3 -2 x 2 +4x+2 x 2 -4x+8)=17
⇔ x 3 -25x - x 3 -8-17=0
⇔ x 3 -25x - x 3 -25=0
⇔-25x-25=0
⇔-25x=25
⇒x=-1
\(\Leftrightarrow x\left(x^2-25\right)-x^3-8=17\\ \Leftrightarrow x^3-25x-x^3=25\\ \Leftrightarrow-25x=25\Leftrightarrow x=-1\)

Để phương trình 1 có 2 nghiệm phân biệt
=> \(\Delta,>0\) <=> \(\left[-\left(m-1\right)\right]^2-\left(-2m+5\right)>0\)
<=>\(\left[{}\begin{matrix}m>2\\m< -2\end{matrix}\right.\)
=> Theo hệ thức Vi ét ta có
\(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\circledast\\x_1.x_2=-2m+5\circledast\circledast\end{matrix}\right.\)
Theo bài ra ta có
\(x_1-x_2=-2\circledcirc\)
Từ \(\circledast vaf\circledcirc\) ta có hệ pt
\(\left\{{}\begin{matrix}x1+x2=2m-2\\x1-x2=-2\end{matrix}\right.\) <=>\(\left\{{}\begin{matrix}x1=m-2\\x2=m\end{matrix}\right.\)
Thay x1 và x2 vào \(\circledast\circledast\)ta dc
\(\left(m-2\right)m=-2m+5\)
<=> m=\(\left[{}\begin{matrix}-\sqrt{5}\\\sqrt{5}\end{matrix}\right.\left(tm\right)\)
Vậy ...
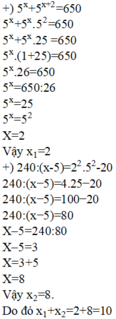

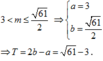



Ta có:
x2-5 là số đối của 5-x2.
\(\Rightarrow\left|x^2-5\right|=\left|5-x^2\right|\)(vì giá tri tuyệt đối sẽ mang cân bằng dấu dương)
\(\Rightarrow2.\left|x^2-5\right|=40\)
\(\left|x^2-5\right|=20\)
Hoặc bằng 20 hoặc bằng -20.
Chúc em học tốt^^
ai mà biết