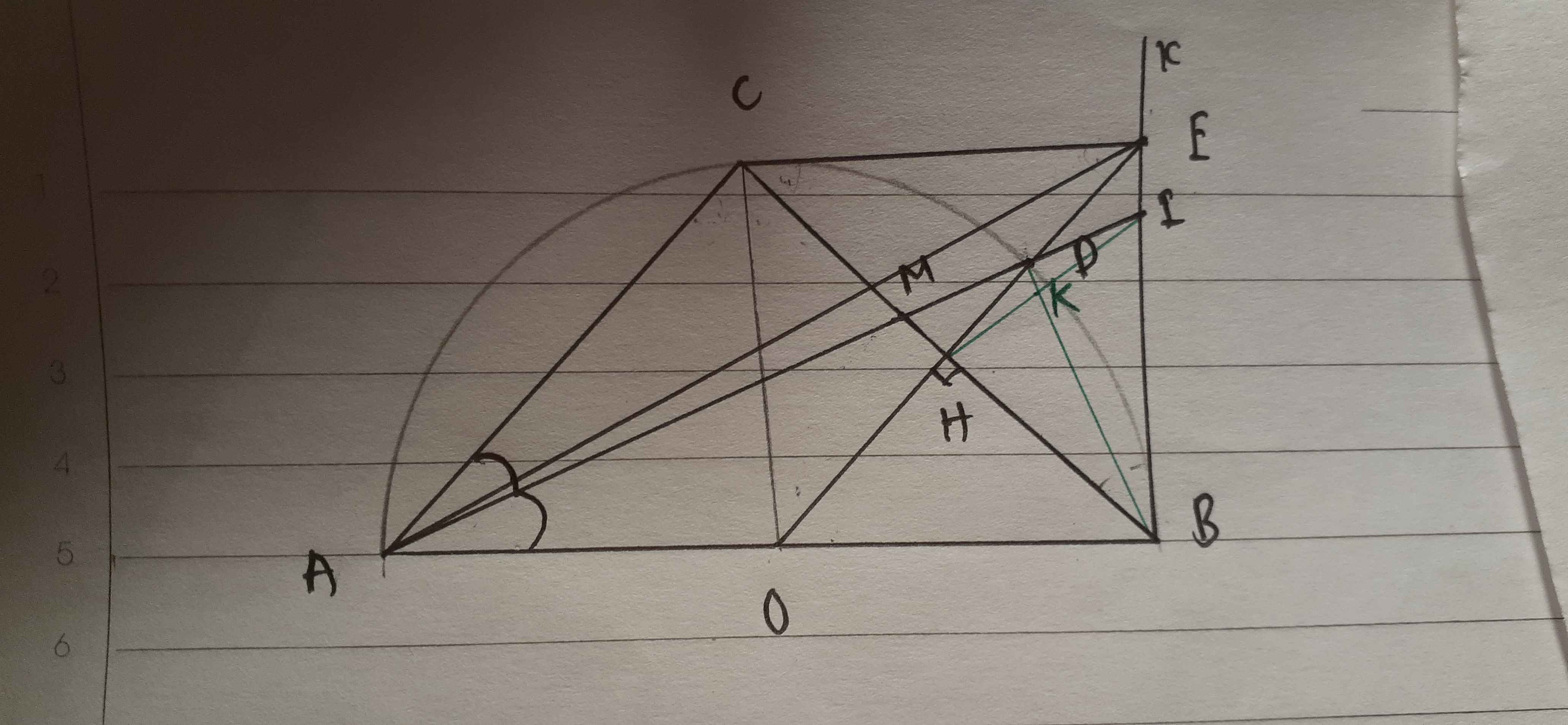
Cho (O) đường kính AB, lấy C thuộc (O), kẻ OH vuông góc BC tại H, tia OH cắt
tiếp tuyến tại B ở E. Gọi D là giao điểm của OE với (O), M là giao điểm của AD
với BC.
b) Chứng minh: EC là tiếp tuyến của (O)
c) Chứng minh: AD là phân giác của CAB
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b: ΔOBC cân tại O có OE là đường cao
nên OE là phân giác của góc COB
Xét ΔBOE và ΔCOE có
OB=OC
góc BOE=góc COE
OE chung
=>ΔBOE=ΔCOE
=>góc OCE=góc OBE=90 độ
=>EC là tiếp tuyến của (O)
c: OB=OC
EB=EC
=>OE là trung trực của BC
=>sđ cung DB=sđ cung DC
=>góc BAD=góc CAD
=>AD là phân giác của góc BAC

Ta có: Tam giác DAO cân tại O (vì OA = OD) => Góc ADO = Góc DAO
Ta lại có: Góc HBD = Góc ADO (cùng phụ Góc HDB) => Góc HBD = Góc DAO
Tam giác DBA vuông tại D => Góc DAB + Góc DBA = 90độ
Mà Góc DBA + Góc DBI = 90độ
=> Góc DAB = Góc DBI hay Góc DAO = Góc DBI
Từ 2 chứng minh trên ta được: Góc HBD = Góc DBI
=> BD (hay BK) là đường phân giác Góc HBI
Áp dụng tính chất đường phân giác vào tam giác BHI ta được:
KH / BH = KI / BI hay KH.BI = KI.BH (đpcm)

a: Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
ΔOBC cân tại O
mà OE là trung tuyến
nên OE vuông góc với BC và OE là phân giác của góc BOC
b: Xét ΔOBD và ΔOCD có
OB=OC
góc BOD=góc COD
OD chung
Do đó: ΔOBD=ΔOCD
=>góc OBD=90 độ
=>DB là tiếp tuyên của (O)