Giúp mình 4 câu này
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


2. I asked the girl to update her lessons.
3. I asked the girl not to learn her lessons parrot-fashion.
4. I asked the girl if she read many books.
5. I asked the girl how many books she bought every year.

\(\frac{75.5^4+175.5^4}{20.25.125-625.75}=\frac{\left(75+175\right).5^4}{4.5.25.5^3-5^4.75}\)
\(=\frac{250.5^4}{100.5^4-5^4.75}=\frac{250.5^4}{\left(100-75\right).5^4}\)
\(=\frac{250}{25}=10\)

Câu 4)
Có 3 dạng cơ năng
- thế năng hấp dẫn : quả bính đang bay
- thế năng đần hồi : lò xo
- động năng : ô tô đang chạy
Câu 5)
Năng lượng vẫn đc bảo toàn và nó chỉ chuyển từ dạng này sang dạng khác

b: Ta có: \(\left(\dfrac{3}{5}-\dfrac{2}{3}x\right)^3=\dfrac{-64}{125}\)
\(\Leftrightarrow\dfrac{3}{5}-\dfrac{2}{3}x=\dfrac{-4}{5}\)
\(\Leftrightarrow x\cdot\dfrac{2}{3}=\dfrac{3}{5}+\dfrac{4}{5}=\dfrac{7}{5}\)
hay \(x=\dfrac{7}{5}:\dfrac{2}{3}=\dfrac{21}{10}\)

Câu 21 :
Số chất là 2 ( Fe2O3,Mg)
\(Fe_2O_3 + 3H_2SO_4\ to Fe_2(SO_4)_3 + 3H_2O\\ Mg + H_2SO_4 \to MgSO_4 + H_2\\ Mg + 2H_2SO_4 \to MgSO_4 + SO_2 + 2H_2O\)


31/
\(3z^2-2z+27=0\)
\(\Delta'=\left(-1\right)^2-3.27=1-3.27=-80\)
\(\Delta'\) có 2 căn bậc 2 là \(\pm4i\sqrt{5}\)
\(\Rightarrow\left\{{}\begin{matrix}z_1=\dfrac{1+4i\sqrt{5}}{3}\\z_2=\dfrac{1-4i\sqrt{5}}{3}\end{matrix}\right.\Rightarrow\left|z_1\right|=\left|z_2\right|=\sqrt{\left(\dfrac{1}{3}\right)^2+\left(\dfrac{4\sqrt{5}}{3}\right)^2}=3\)
\(\Rightarrow z_1\left|z_2\right|+z_2\left|z_1\right|=1+4i\sqrt{5}+1-4i\sqrt{5}=2\) => A
32/ \(\Delta'=4-29=-25\Rightarrow\left\{{}\begin{matrix}z_1=-2+5i\\z_2=-2-5i\end{matrix}\right.\Rightarrow\left|z_1\right|=\left|z_2\right|=\sqrt{2^2+5^2}=\sqrt{29}\)
\(\Rightarrow\left|z_1\right|^4+\left|z_2\right|^4=2.\sqrt{29^4}=1682\) => B
33/ \(\Delta=1-12=-11\Rightarrow\left\{{}\begin{matrix}z_1=\dfrac{1+i\sqrt{11}}{6}\\z_2=\dfrac{1-i\sqrt{11}}{6}\end{matrix}\right.\Rightarrow\left|z_1\right|=\left|z_2\right|=\sqrt{\left(\dfrac{1}{6}\right)^2+\left(\dfrac{\sqrt{11}}{6}\right)^2}=\dfrac{\sqrt{3}}{3}\)
\(\Rightarrow\left|z_1\right|+\left|z_2\right|=\dfrac{2\sqrt{3}}{3}\) => D
34/ \(\Delta=1-4.3.2=-23\Rightarrow\left\{{}\begin{matrix}z_1=\dfrac{1-i\sqrt{23}}{6}\\z_2=\dfrac{1+i\sqrt{23}}{6}\end{matrix}\right.\Rightarrow\left|z_1\right|=\left|z_2\right|=\sqrt{\dfrac{1}{36}+\dfrac{23}{36}}=\dfrac{\sqrt{6}}{3}\)
\(\Rightarrow T=2.\left(\dfrac{\sqrt{6}}{3}\right)^2=\dfrac{4}{3}\) => C

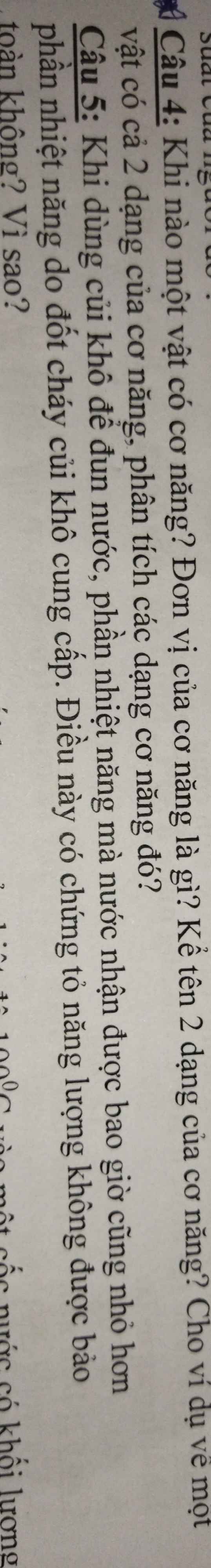
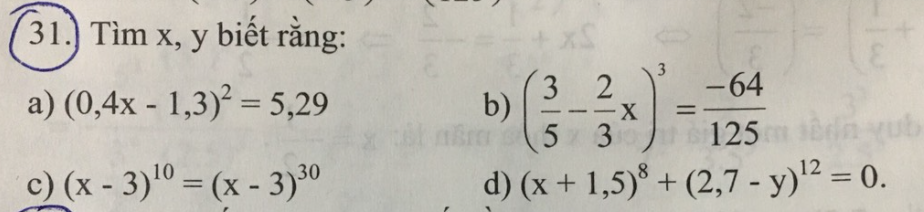 giúp mình 4 câu này với mình đang cần gấp
giúp mình 4 câu này với mình đang cần gấp 


 giúp mình 4 câu này nhanh ạ
giúp mình 4 câu này nhanh ạ

7.
\(\sqrt{4-x}\ge0\Rightarrow\sqrt{4-x}+\sqrt{3}\ge\sqrt{3}\) đáp án D
8.
\(y=x^2+\dfrac{1}{2x}+\dfrac{1}{2x}\ge3\sqrt[3]{\dfrac{x^2}{4x^2}}=\dfrac{3}{\sqrt[3]{4}}\)
Dấu "=" xảy ra khi \(x^2=\dfrac{1}{2x}\Leftrightarrow x=\dfrac{1}{\sqrt[3]{2}}\) đáp án D
9.
\(y\ge2\sqrt{\dfrac{2x}{x}}-\left(1+\sqrt{2}\right)^2=2\sqrt{2}-\left(3+2\sqrt{2}\right)=-3\) đáp án B
10.
\(y'=\dfrac{1-2x}{\left(x-2\right)^2\sqrt{x^2-1}}\Rightarrow\) hàm đồng biến trên \((-\infty;-1]\) và nghịch biến trên \(\left[1;\dfrac{3}{2}\right]\)
\(f\left(-1\right)=f\left(1\right)=0\) ; \(f\left(\dfrac{3}{2}\right)=-\sqrt{5}\)
\(\Rightarrow f\left(x\right)_{max}=0\) ; \(f\left(x\right)_{min}=-\sqrt{5}\) đáp án A
11.
\(f'\left(x\right)=\dfrac{5-x}{\left(x^2+2\right)\sqrt{x^2+5}}=0\Rightarrow x=5\) \(\Rightarrow f\left(5\right)=\dfrac{\sqrt{30}}{5}\)
\(\lim\limits_{x\rightarrow+\infty}f\left(x\right)=1\) ; \(\lim\limits_{x\rightarrow-\infty}f\left(x\right)=-1\)
Hàm đạt GTLN tại \(x=5\) và ko có GTNN, đáp án D