Cho tam giác ABC. M là trung điểm của BC. Trên tia đối của tia MA lấy điểm E sao cho ME = MA.
chứng minh rằng a)AB=CE b)AC//BE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
V
6 tháng 8 2017
a) Xét ΔMAB và ΔMEC có
MB=MC (M là trung điểm BC)
^AMB=^EMC ( đối đỉnh)
MA= ME (gt)
Vậy ΔMAB = ΔMEC
b)Chứng minh ΔAMC= ΔBME tương tự câu (a)
Suy ra được ^CAM=^MEB
Do đó AC//BE
NC
8 tháng 1 2021
Xét ABM và EMC có : AM = ME BM = CM Góc AMB = góc CME ( đối đỉnh ) => tam giac ABM = Tam giác EMC Ta có : Tam giác AMB = tam giác EMC nên góc BAM = góc EMC Mặt khác : 2 góc BAM và AEC nắm vị trí so le trong => AB // CE c Xét tam giác AIB và tam gics CIK có : AI = IC BI = Ik Góc AIB = góc CIK ( đối đỉnh ) => tam giác AIB = tam giác CIK
CG
25 tháng 1 2017
a)XÉT TAM GIÁC ABM VÀ TAM GIÁC ECM CÓ:
BM= CM ( M LÀ TRUNG ĐIỂM CỦA BC)
GÓC BMA = GÓC CME( 2 GÓC ĐỐI ĐỈNH)
AM = EM ( GT)
=> TAM GIÁC ABM = TAM GIÁC ECM( C-G-C)
b) CÓ TAM GIÁC ABM = TAM GIÁC ECM( CM Ở CÂU a)
SUY RA GÓC ABM = GÓC ECM( HAI GÓC TƯƠNG ỨNG)
MÀ 2 GÓC NÀY NẰM Ở VỊ TRÍ SO LE TRONG
=> AB//CE( DNNB 2 ĐƯỜNG THẲNG //)
OK NHỚ KIIK CHO MÌNH NHA
NĂM MỚI ZUI ZẺ
TA
20 tháng 7 2023
a) Xét tam giác ABM và tam giác ECM
Có:
AM = EM (gt)
BM = MC (gt)
AE cạnh chung
=> Tam giác ABM = tam gicas ECM (c.c.c)
b) Ta có: Tam giác ABM = tam giác ECM
=> AB = Ce (2 cạnh t/ư)
Tiếp theo bạn kẻ thêm rồi xét 2 tam giác ACM và tam giác BME (tương tự như câu A th) nhé (cả hình giống hình thoi nhé)
Từ đó có tam giác ACM = tam giác BME
=> Góc AMC = góc BME (2 góc đối đỉnh)
=> AC//BE (đpcm)
:))
21 tháng 7 2023
a: Xét ΔABM và ΔECM có
MA=ME
góc AMB=góc EMC
MB=MC
=>ΔABM=ΔECM
b: ΔABM=ΔECM
=>AB=CE
Xét tứ giác ABEC có
M là trung điểm chung của AE và bC
=>ABEC là hình bình hành
=>AC//BE
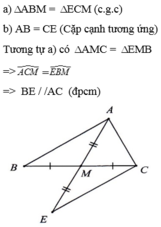
Hình tự vẽ nha !
a/ Xét ΔABM và ΔECM có:
MB=MC (Mlà trung điểm của BC)
góc AMB = góc EMC ( 2 góc đối đỉnh)
MA=ME(giả thiết)
Do đó ΔABM=ΔECM(c.g.c)
b/ vì ΔABM=ΔECM nên góc BAM= góc MEC (2 góc tương ứng)
mà góc BAM và góc MEC là 2 góc ở vị trí so le trong ( khi đoạn thẳng AE cắt AB và CE ở A và E) nên theo dấu hiệu nhận biết 2 đường thẳng song song => AB // CE
c/ mik ko bt