Các phân số/;1/5;3/2;1/4 được xếp theo thứ tự từ lớn đến bé là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
20 tháng 11 2018
a) Rút gọn phân số:
b) Viết các phân số đều có mẫu số là 40 và bằng các phân số đã cho:
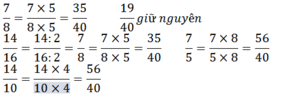
c)Trong các phân số trên có những phân số bằng nhau là:
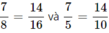và 
31 tháng 1 2023
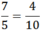
a. Các phân số bé hơn 1:
2/3 ; 3/4; 4/5; 2/4; 2/5; 3/5
b. Các phân số lớn hơn 1:
3/2; 4/3; 5/4 ; 4/2; 5/2; 5/3
c. Các phân số bằng 1:
2/2; 3/3; 4/4; 5/5
CM
17 tháng 11 2017
Các phân số có mẫu số là 10,100,1000 được gọi là phân số thập phân.
Mà trong các phân số trên ta thấy số phân số 7 10 có mẫu số la 10. Vậy phân số 7 10 là phân số thập phân.
Đáp án cần chọn là C
28 tháng 6 2023
Gọi \(q_1,q_2,...,q_n\left(q_i\inℚ,\forall i=\overline{1,n}\right)\). Theo đề bài, ta có \(q_1q_2...q_n\inℤ\) và \(q_i+q_j\inℤ,\forall i\ne j;i,j=\overline{1,n}\). Không mất tính tổng quát, giả sử \(q_1< q_2< ...< q_n\)
Ta thấy \(q_1+q_2\inℤ\) và \(q_2+q_3\inℤ\) nên \(q_1-q_3\inℤ\). Mà \(q_1+q_3\inℤ\) nên nếu ta đặt \(q_1-q_3=v\) và \(q_1+q_3=u\) với \(u,v\inℤ\) thì \(q_1=\dfrac{u+v}{2};q_3=\dfrac{u-v}{2}\). Do \(q_1+q_2=\dfrac{u+v+2q_2}{2}\) và \(q_3+q_2=\dfrac{u-v+2q_2}{2}\) cũng là các số nguyên, hơn nữa \(u-v\equiv u+v\left(mod2\right)\) nên ta chỉ cần suy ra \(u+v+2q_1⋮2\) hay \(u+v\) là số chẵn, cũng tức là \(q_1=\dfrac{u+v}{2}\) là số nguyên. Một cách tương tự, ta sẽ chứng minh được \(q_i\inℤ,\forall i=\overline{1,n}\) (đpcm)
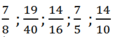
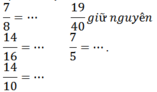
3/2; 1/4; 1/5
3/2 , 1/4 , 1/5