Tam giác ABC cân tại A Các đường phân giác BD và Ce:CMR BEDC là hình thang cân có đáy nhỏ bằng cạnh trên( giúp tui với mới học nên chưa quen)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bạn vào
Giúp tôi giải toán - Hỏi đáp, thảo luận về toán học - Học toán với OnlineMath
a: Xét ΔADB và ΔAEC có
góc BAD chung
AB=AC
góc ABD=góc ACE
Do đó: ΔADB=ΔAEC
b: Xét ΔABC có AE/AB=AD/AC
nên ED//BC
=>BEDC là hình thang
mà góc EBC=góc DCB
nên BEDC là hình thang cân
Xét ΔEDB có góc EDB=góc EBD(=góc DBC)
nên ΔEDB cân tại E
=>BE=ED=DC

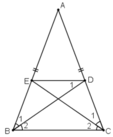
- Chứng minh tứ giác BCDE là hình thang cân:
+ ΔABC cân tại A 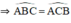
BD là phân giác của 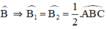
CE là phân giác của 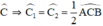
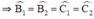
+ Xét ΔAEC và ΔADB có:
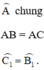
⇒ ΔAEC = ΔADB
⇒ AE = AD
Vậy tam giác ABC cân tại A có AE = AD
Theo kết quả bài 15a) suy ra BCDE là hình thang cân.
- Chứng minh ED = EB.
ED // BC ⇒ 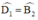 (Hai góc so le trong)
(Hai góc so le trong)
Mà 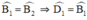 ⇒ ΔEDB cân tại E ⇒ ED = EB.
⇒ ΔEDB cân tại E ⇒ ED = EB.
Vậy ta có EBCD là hình thang cân có đáy nhỏ bằng cạnh bên.

- Chứng minh tứ giác BCDE là hình thang cân:
+ \(\Delta ABC\)cân tại A \(\Rightarrow\widehat{ABC}=\widehat{ACB}\)
BD là tia phân giác của \(\widehat{B}\Rightarrow\widehat{B_1}=\widehat{B_2}=\frac{1}{2}.\widehat{ABC}\)
CE là tia phân giác của \(\widehat{C}\Rightarrow\widehat{C_1}=\widehat{C_2}=\frac{1}{2}.\widehat{ACB}\)
\(\Rightarrow\widehat{B_1}=\widehat{B_2}=\widehat{C_1}=\widehat{C_2}\)
+) Xét 2 tam giác : AEC và ADB , có :
\(\widehat{A}\)chung
AB = AC
\(\widehat{C_1}=\widehat{B_1}\)
\(\Rightarrow\Delta AEC=\Delta ADB\left(g.c.g\right)\)
=> AE = AD ( 2 cạnh tương ứng )
Ta có : AD = AE ( cmt ) nên tam giác ADE cân tại A ( dấu hiệu nhận biết tam giác cân )
\(\Rightarrow\widehat{AED}=\widehat{ADE}\)( tính chất tam giác cân )
Xét tam giác ADE , ta có :
\(\widehat{AED}+\widehat{ADE}+\widehat{A}=180^o\)( định lý tổng 3 góc trong tam giác )
\(\Rightarrow2\widehat{AED}+\widehat{A}=180^o\)
\(\Rightarrow\widehat{AED}=\frac{180^o-\widehat{A}}{2}\left(1\right)\)
Xét tam giác ABC , ta có :
\(\widehat{A}+\widehat{ABC}+\widehat{ACB}=180^o\)( định lý tổng 3 góc trong tam giác )
Mà \(\widehat{ABC}=\widehat{ACB}\left(cmt\right)\)
\(\Rightarrow2\widehat{ABC}+\widehat{A}=180^o\)
\(\Rightarrow\widehat{ABC}=\frac{180^o-\widehat{A}}{2}\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\widehat{AED}=\widehat{ABC}\), mà hai góc này là hai góc đồng vị nên suy ra DE // BC ( dấu hiệu nhận biết hai đường thẳng song song )
Do đó BEDC là hình thang (dấu hiệu nhận biết hình thang).
Lại có\(\widehat{ABC}=\widehat{ACB}\) (chứng minh trên)
Nên BEDC là hình thang cân (dấu hiệu nhận biết hình thang cân)
Ta có:
DE // BC => \(\widehat{D_1}=\widehat{B_2}\) (so le trong)
Lại có \(\widehat{B_2}=\widehat{B_1}\) ( cmt ) nên \(\widehat{B_1}=\widehat{D_1}\)
\(\Rightarrow\Delta EBD\) cân tại E (dấu hiệu nhận biết tam giác cân)
=> EB = ED ( tính chất tam giác cân )
Vậy BEDC là hình thang cân có đáy nhỏ bằng cạnh bên.

Ta có : tam giác ABC cân tại A
BD là phân giác của góc ABC
CE là phân giác của góc ACB
=>BD=CE (trong tam giác cân 2 đường phân giác xuất phát từ 2 góc đáy của tam giác bằng nhau . p/s: nếu bạn k bik định lí này bạn có thể chứng minh nhé)
Xét tam giác ABD và tam giác ACE :
BD=CE (cmt)
góc ABD= góc ACE (góc ABC=góc ACB=2 góc ABD= 2 góc ACE)
AB=BC (tam giác ABC cân tại A)
Suy ra: tam giác ABD= tam giác ACE (c-g-c)
=>AD=AE ( 2 cạnh tương ứng)
=>tam giác ADE cân tại A
Mà tam giác ABC cũng cân tại A nên:
góc ABC = góc ACB= góc ADE= goác ADE
Ta lại có: góc ABC và góc AED ở vị trí đồng vị nên:
ED//BC
=>BEDC là hình thang
Mà BD=CE
nên: BEDC là hình thang cân(1)
Ta có: ED//BC => góc DEC = góc ECB
Mà góc ECB= góc DCE ( CE là p/g của góc ACE)
=> góc DEC=góc DCE
=> tam giác DEC cân tại D
=>ED=DC (2)
Từ (1) và (2) suy ra: BEDC là hình thang cân có đáy nhò bằng cạnh bên.
Hok tốt ! Nếu thấy đúng thì k cho mìn !

Ta có : tam giác ABC cân tại A
BD là phân giác của góc ABC
CE là phân giác của góc ACB
=>BD=CE (trong tam giác cân 2 đường phân giác xuất phát từ 2 góc đáy của tam giác bằng nhau . p/s: nếu bạn k bik định lí này bạn có thể chứng minh nhé)
Xét tam giác ABD và tam giác ACE :
BD=CE (cmt)
góc ABD= góc ACE (góc ABC=góc ACB=2 góc ABD= 2 góc ACE)
AB=BC (tam giác ABC cân tại A)
Suy ra: tam giác ABD= tam giác ACE (c-g-c)
=>AD=AE ( 2 cạnh tương ứng)
=>tam giác ADE cân tại A
Mà tam giác ABC cũng cân tại A nên:
góc ABC = góc ACB= góc ADE= goác ADE
Ta lại có: góc ABC và góc AED ở vị trí đồng vị nên:
ED//BC
=>BEDC là hình thang
Mà BD=CE
nên: BEDC là hình thang cân(1)
Ta có: ED//BC => góc DEC = góc ECB
Mà góc ECB= góc DCE ( CE là p/g của góc ACE)
=> góc DEC=góc DCE
=> tam giác DEC cân tại D
=>ED=DC (2)
Từ (1) và (2) suy ra: BEDC là hình thang cân có đáy nhò bằng cạnh bên.
Bài b ko biết hi hi k mình ra
Tiếp câu b .
Có : \(\Delta ABC\) cân tại A
=> \(\widehat{ABC}=\widehat{ACB}\) (1)
Theo tổng 3 góc trong 1 tam giác :
Với \(\Delta ABC\) => \(\widehat{ABC}+\widehat{ACB}+\widehat{A}=180^0\)
=> \(\widehat{ABC}+\widehat{ACB}=130^0\)
Lại có (1)
=> \(\widehat{ABC}=\widehat{ACB}=\frac{130^0}{2}=65^0\)
Vì tứ giác là hình thang cân (chắc cũng biết tứ giác nào nhỉ :v )
=> ED // BC
=> \(\widehat{DEB}+\widehat{EBC}=180^0\)
=> \(\widehat{DEB}=180^0-65^0=115^0\)
Tương tự với góc \(\widehat{EDC}\)
\(\Delta\)BEC = \(\Delta\)CDB (g.c.g)
=> Góc B = góc C
Vậy tứ giác BEDC có 2 góc kề 1 dáy nên là hình thang cân
:) hình như sai đề bằng cạnh bên mới đúng