Question

[Nguyễn Gia Bảo]

Cho tam giác ABC vuông tại A. Trên cạnh AC lấy điểm M (M ≠ A, M ≠ C). Từ C vẽ đường thẳng vuông góc với tia BM, đường thẳng này cắt tia BM tại D và cắt tia BA tại E.

a) chứng minh tam giác EAC đồng dạng với tam giác EDB.

b) biết diện tích tam giác AED=50 cm², góc EBD=30^o.

    Tính diện tích tam giác EBC

Answer 1

[Nguyễn Lê Phước Thịnh]

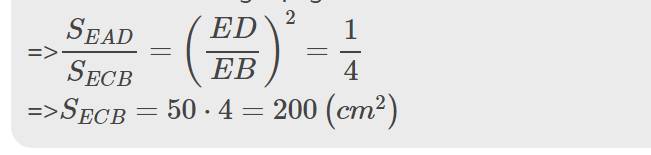
a: Xét ΔEAC vuông tại A và ΔEDB vuông tại D có

\(\widehat{AEC}\) chung

Do đó: ΔEAC đồng dạng với ΔEDB

b: Ta có: ΔEDB vuông tại D

=>\(\widehat{DEB}+\widehat{DBE}=90^0\)

=>\(\widehat{DEB}=60^0\)

Xét ΔEDB vuông tại D có \(cosE=\dfrac{ED}{EB}\)

=>\(\dfrac{ED}{EB}=cos60=\dfrac{1}{2}\)

Ta có: ΔEAC đồng dạng với ΔEDB

=>\(\dfrac{EA}{ED}=\dfrac{EC}{EB}\)

=>\(\dfrac{EA}{EC}=\dfrac{ED}{EB}\)

Xét ΔEAD và ΔECB có

EA/EC=ED/EB

góc E chung

Do đó: ΔEAD đồng dạng với ΔECB

=>\(\dfrac{S_{EAD}}{S_{ECB}}=\left(\dfrac{ED}{EB}\right)^2=\dfrac{1}{4}\)

=>\(S_{ECB}=50\cdot4=200\left(cm^2\right)\)