Giải phương trình chứa ẩn ở mẫu:
a x-1/x+3 - x/x-3 = 7x-3/9-x2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 2 2021
Giải phương trình chứa ẩn ở mẫu:a) 4x 2/3x-6-x/2-x=1 3x/2x-4b) x-3/x 3-x 3/x-3=3/x2-9Các bạn hãy giúp mik với:))
PT
1
16 tháng 6 2022
1: \(\dfrac{x+6}{x-5}+\dfrac{x-5}{x+6}=\dfrac{2x^2+23x+61}{x^2+x-30}\)
\(\Leftrightarrow x^2+12x+36+x^2-10x+25=2x^2+23x+61\)
=>23x+61=2x+61
hay x=0
2: \(\dfrac{6}{x-5}+\dfrac{x+2}{x-8}=\dfrac{18}{\left(x-5\right)\left(8-x\right)}-1\)
\(\Leftrightarrow6x-48+x^2-3x-10=-18-x^2+13x-40\)
\(\Leftrightarrow x^2+3x-58+x^2-13x+58=0\)
\(\Leftrightarrow2x^2-10x=0\)
=>2x(x-5)=0
=>x=0
c: \(\dfrac{x^2-x}{x+3}-\dfrac{x^2}{x-3}=\dfrac{7x^2-3x}{9-x^2}\)
\(\Leftrightarrow\left(x^2-x\right)\left(x-3\right)-x^2\left(x+3\right)=-7x^2+3x\)
\(\Leftrightarrow x^3-3x^2-x^2+3x-x^3-3x^2+7x^2-3x=0\)
\(\Leftrightarrow x^2=0\)
hay x=0
DT
18 tháng 2 2022
a, \(\Leftrightarrow\left(9x^2-4\right)\left(x+1\right)-\left(3x+2\right)\left(x-1\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(\left(9x^2-4\right)-\left(\left(3x+2\right)\left(x-1\right)\right)\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(9x^2-4-\left(3x^2-x-2\right)\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(9x^2-4-3x^2+x+2\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(3x^2+x-2\right)=0\)
\(\Leftrightarrow\left(x+1\right)=0;3x^2+x-2=0\)
=> x=-1
với \(3x^2+x-2=0\)
ta sử dụng công thức bậc 2 suy ra : \(x=\dfrac{2}{3};x=-1\)
Vậy ghiệm của pt trên \(S\in\left\{-1;\dfrac{2}{3}\right\}\)
18 tháng 2 2022
b: \(\Leftrightarrow x^2-2x+1-1+x^2=x+3-x^2-3x\)
\(\Leftrightarrow2x^2-2x=-x^2-2x+3\)
\(\Leftrightarrow3x^2=3\)
hay \(x\in\left\{1;-1\right\}\)
c: \(\Leftrightarrow\left(x-1\right)\left(x+1\right)\left(x+2\right)\left(x-3\right)-\left(x-1\right)\left(x-2\right)\left(x+2\right)\left(x+5\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)\left[\left(x+1\right)\left(x-3\right)-\left(x-2\right)\left(x+5\right)\right]=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)\left(x^2-2x-3-x^2-3x+10\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)\left(-5x+7\right)=0\)
hay \(x\in\left\{1;-2;\dfrac{7}{5}\right\}\)
CM
20 tháng 11 2019
a)
3 · x 2 + x 2 - 2 x 2 + x - 1 = 0 ( 1 )
Đặt t = x 2 + x ,
Khi đó (1) trở thành : 3 t 2 – 2 t – 1 = 0 ( 2 )
Giải (2) : Có a = 3 ; b = -2 ; c = -1
⇒ a + b + c = 0
⇒ (2) có hai nghiệm t 1 = 1 ; t 2 = c / a = - 1 / 3 .
+ Với t = 1 ⇒ x 2 + x = 1 ⇔ x 2 + x – 1 = 0 ( * )
Có a = 1; b = 1; c = -1 ⇒ Δ = 1 2 – 4 . 1 . ( - 1 ) = 5 > 0
(*) có hai nghiệm
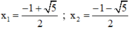
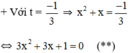
Có a = 3; b = 3; c = 1 ⇒ Δ = 3 2 – 4 . 3 . 1 = - 3 < 0
⇒ (**) vô nghiệm.
Vậy phương trình (1) có tập nghiệm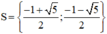 
b)
x 2 − 4 x + 2 2 + x 2 − 4 x − 4 = 0 ⇔ x 2 − 4 x + 2 2 + x 2 − 4 x + 2 − 6 = 0 ( 1 )
Đặt x 2 – 4 x + 2 = t ,
Khi đó (1) trở thành: t 2 + t – 6 = 0 ( 2 )
Giải (2): Có a = 1; b = 1; c = -6
⇒ Δ = 1 2 – 4 . 1 . ( - 6 ) = 25 > 0
⇒ (2) có hai nghiệm
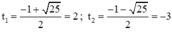
+ Với t = 2 ⇒ x 2 – 4 x + 2 = 2
⇔ x 2 – 4 x = 0
⇔ x(x – 4) = 0
⇔ x = 0 hoặc x = 4.
+ Với t = -3 ⇒ x 2 – 4 x + 2 = - 3
⇔ x2 – 4x + 5 = 0 (*)
Có a = 1; b = -4; c = 5 ⇒ Δ ’ = ( - 2 ) 2 – 1 . 5 = - 1 < 0
⇒ (*) vô nghiệm.
Vậy phương trình ban đầu có tập nghiệm S = {0; 4}.
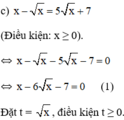
Khi đó (1) trở thành: t 2 – 6 t – 7 = 0 ( 2 )
Giải (2): Có a = 1; b = -6; c = -7
⇒ a – b + c = 0
⇒ (2) có nghiệm t 1 = - 1 ; t 2 = - c / a = 7 .
Đối chiếu điều kiện chỉ có nghiệm t = 7 thỏa mãn.
+ Với t = 7 ⇒ √x = 7 ⇔ x = 49 (thỏa mãn).
Vậy phương trình đã cho có nghiệm x = 49.
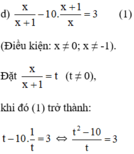
⇔ t 2 – 10 = 3 t ⇔ t 2 – 3 t – 10 = 0 ( 2 )
Giải (2): Có a = 1; b = -3; c = -10
⇒ Δ = ( - 3 ) 2 - 4 . 1 . ( - 10 ) = 49 > 0
⇒ (2) có hai nghiệm:
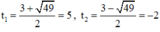
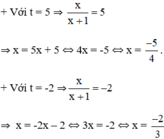
Cả hai nghiệm đều thỏa mãn điều kiện xác định.
Vậy phương trình đã cho có tập nghiệm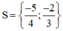 
14 tháng 4 2020
1, Các bước giải phương trình chứa ẩn ở mẫu:
Bước 1: Tìm ĐKXĐ của phương trình
Bước 2: Quy đồng và khử mẫu phương trình
Bước 3: Giải phương trình đã khử mẫu
Bước 4: Đối chiếu nghiệm với ĐKXĐ
2, Bạn kiểm tra lại đề
PT
Cho phương trình ẩn x: x + a a - x + x - a a + x = a 3 a + 1 a 2 - x 2
Giải phương trình khi a = - 3
1
CM
8 tháng 2 2019
Khi a = - 3, ta có phương trình:
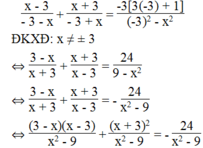
⇔ (3 – x)(x – 3) + x + 3 2 = -24
⇔ 3x – 9 – x 2 + 3x + x 2 + 6x + 9 = -24 ⇔ 12x = - 24
⇔ x = -2 (thỏa mãn)
Vậy phương trình có nghiệm x = -2
HP
11 tháng 1 2022
\(a.\left(3x+2\right)\left(x^2-1\right)=\left(9x^2-4\right)\left(x+1\right)\)
\(\Leftrightarrow\left(3x+2\right)\left(x+1\right)\left(x-1\right)=\left(3x-2\right)\left(3x+2\right)\left(x+1\right)\)
\(\Leftrightarrow x-1=3x-2\)
\(\Leftrightarrow2x=1\)
\(\Leftrightarrow x=\dfrac{1}{2}\)
11 tháng 1 2022
c: =>x-3=0
hay x=3
d: \(\Leftrightarrow\left(3x-1\right)\cdot\left(x^2+2-7x+10\right)=0\)
\(\Leftrightarrow\left(3x-1\right)\left(x-3\right)\left(x-4\right)=0\)
hay \(x\in\left\{\dfrac{1}{3};3;4\right\}\)
11 tháng 1 2022
\(\left(3x+2\right)\left(x^2-1\right)=\left(9x^2-4\right)\left(x+1\right).\)
\(\Leftrightarrow\left(3x+2\right)\left(x-1\right)\left(x+1\right)-\left(3x-2\right)\left(3x+2\right)\left(x+1\right)=0.\)
\(\Leftrightarrow\left(3x+2\right)\left(x+1\right)\left(x-1-3x+2\right)=0.\)
\(\Leftrightarrow\left(3x+2\right)\left(x+1\right)\left(-2x+1\right)=0.\)
\(\Leftrightarrow\left[{}\begin{matrix}3x+2=0.\\x+1=0.\\-2x+1=0.\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{2}{3}.\\x=-1.\\x=\dfrac{1}{2}.\end{matrix}\right.\)
11 tháng 1 2022
c: =>(x-3)(x2+3x+5)=0
=>x-3=0
hay x=3
d: =>(3x-1)(x2+2-7x+10)=0
=>(3x-1)(x-3)(x-4)=0
hay \(x\in\left\{\dfrac{1}{3};3;4\right\}\)
\(\frac{x-1}{x+3}-\frac{x}{x-3}=\frac{7x-3}{9-x^2}\)ĐK : \(x\ne\pm3\)
\(\Leftrightarrow\frac{x-1}{x+3}+\frac{x}{3-x}=\frac{7x-3}{9-x^2}\)
\(\Leftrightarrow\frac{\left(x-1\right)\left(3-x\right)+x\left(x+3\right)}{\left(x+3\right)\left(3-x\right)}=\frac{7x-3}{\left(3-x\right)\left(x+3\right)}\)
\(\Rightarrow3x-x^2-3+x+x^2+3x=7x-3\)
\(\Leftrightarrow7x-3=7x-3\Leftrightarrow0x=0\)
Vậy phương trình có vô số nghiệm
Trả lời:
\(\frac{x-1}{x+3}-\frac{x}{x-3}=\frac{7x-3}{9-x^2}\)\(\left(ĐKXĐ:x\ne\pm3\right)\)
\(\Leftrightarrow\frac{x-1}{x+3}-\frac{x}{x-3}=\frac{3-7x}{x^2-9}\)
\(\Leftrightarrow\frac{\left(x-1\right)\left(x-3\right)}{x^2-9}-\frac{x\left(x+3\right)}{x^2-9}=\frac{3-7x}{x^2-9}\)
\(\Rightarrow x^2-3x-x+3-\left(x^2+3x\right)=3-7x\)
\(\Leftrightarrow x^2-4x+3-x^2-3x=3-7x\)
\(\Leftrightarrow3-7x=3-7x\)
\(\Leftrightarrow-7x+7x=3-3\)
\(\Leftrightarrow0x=0\)( luôn thỏa mãn )
Vậy \(S=ℝ\)với \(x\ne\pm3\)