Cho tam giác ABC cân tại A. Trên nửa mặt phẳng bờ BC không chưa A, vẽ tam giác đều BCD. Tính số đó BDA.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vì tam giác BCD là tam giác đều nên góc BDC =600
Xét tam giác BAD và tam giác CAD có
BA = CA (tam giác ABC cân tại A)
BD =CD (tam giác BCD là tam giác đều)
AD : cạnh chung
Do đó : tam giác BAD = tam giác CAD (c.c.c) => góc BDA = góc CDA (2 góc t/ứng ). Mà góc BDC =600 => góc BDA = góc CDA=300
Vậy góc BDA =300
Cho mk nhìu nhìu k nha .mk cảm ơn A B C D
A B C D
ta có tam giác ABC cân tại A nên AB=AC
tam giác BDC đều nên BD=CD
Xét tam giác ABD và tam giác ACD có :
AB=AC (chứng minh trên)
chung cạnh AD
BD=CD(chứng minh trên)
nên ABD=BCD(C-C-C)=>góc BDA=góc CDA=1/2 góc BDC=>BDA=300

vì tam giác ABC cân tại A => AB = AC
tam giác BCD đều => BD = DC
xét tam giác ABD và tam giác ACD có:
AB =AC ( cmt)
BD = DC (cmt)
AD chung
từ 3 điều trên => tam giác ABD = tam giác ACD ( c.c.c)
=> góc ADB = Góc ADC => DA là tia phân giác góc BDC.
=> góc BDA = góc BDC/ 2 = 60 độ / 2 = 30 độ.

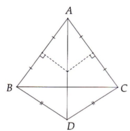
Từ giả thiết, ta có: AB = AC, DB = DC.
=> AD là đường trung trực của BC.
Xét tam giác ABC, theo tính chất ba đường trung trực trong tam giác ta có các đường trung trực của AB và AC đồng quy với đường thẳng AD.

Vì tam giác ABC cân tại A => AB = AC
Tam giác BCD đều => BD = DC
Xét tam giác ABD và tam giác ACD có:
AB = AC (cmt)
BD = DC (cmt)
AD chung
Từ 3 điều trên => tam giác ABD = tam giác ACD (c.c.c)
=> Góc ADB = góc ADC => DA là tia phân giác góc BDC
=> Góc BDA = góc BDC / 2 = 60 độ / 2 = 30 độ