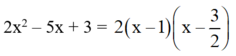Cho pt ax2+bx+c=0 có 2 nghiệm x1,x2 thoả mãn x1=x22.Chứng minh rằng : b3+a2c+ac2=3abc
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


theo bài ra ta có
n = 8a +7=31b +28
=> (n-7)/8 = a
b= (n-28)/31
a - 4b = (-n +679)/248 = (-n +183)/248 + 2
vì a ,4b nguyên nên a-4b nguyên => (-n +183)/248 nguyên
=> -n + 183 = 248d => n = 183 - 248d (vì n >0 => d<=0 và d nguyên )
=> n = 183 - 248d (với d là số nguyên <=0)
vì n có 3 chữ số lớn nhất => n<=999 => d>= -3 => d = -3
=> n = 927

\(ax^2+bx+c=0\)
Theo định lý Viet
\(\Rightarrow\left\{{}\begin{matrix}S=x_1+x_2=\dfrac{-b}{a}\\P=x_1x_2=\dfrac{c}{a}\end{matrix}\right.\)
Ta có pt bậc 2 có 2 nghiệm là \(\dfrac{1}{x^2_1};\dfrac{1}{x^2_2}\)
\(\Rightarrow\left\{{}\begin{matrix}S'=\dfrac{1}{x^2_1}+\dfrac{1}{x^2_2}\\P'=\dfrac{1}{x^2_1x^2_2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}S'=\dfrac{\left(x_1+x_2\right)^2-2x_1x_2}{x^2_1x^2_2}\\P'=\dfrac{1}{x^2_1x^2_2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}S'=\dfrac{\left(\dfrac{-b}{a}\right)^2-\dfrac{2c}{a}}{\left(\dfrac{c}{a}\right)^2}\\P'=\dfrac{1}{\left(\dfrac{c}{a}\right)^2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}S'=\dfrac{\dfrac{b^2}{a^2}-\dfrac{2c}{a}}{\dfrac{c^2}{a^2}}\\P'=\dfrac{1}{\dfrac{c^2}{a^2}}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}S'=\dfrac{\dfrac{b^2-2ca}{a^2}}{\dfrac{c^2}{a^2}}=\dfrac{b^2-2ca}{c^2}\\P'=\dfrac{a^2}{c^2}\end{matrix}\right.\)
Theo định lý Viet đảo pt bậc 2 cần lập
\(\Leftrightarrow z^2-S'z+P'=0\)
\(\Leftrightarrow z^2-\dfrac{b^2-2ca}{c^2}z+\dfrac{a^2}{c^2}=0\)

a)Ta có:
`\Delta'`
`=(m+1)^2-6m+4`
`=m^2+2m+1-6m+4`
`=m^2-4m+5`
`=(m-2)^2+1>=1>0(AA m)`
`=>`phương trình (1) luôn có 2 nghiệm phân biệt với mọi m
Câu b đề không rõ :v

3x2 + 8x + 2 = 0
Có a = 3; b' = 4; c = 2
⇒ Δ’ = 42 – 2.3 = 10 > 0
⇒ Phương trình có hai nghiệm phân biệt:


* Chứng minh:
Phương trình a x 2 + b x + c = 0 có hai nghiệm x 1 ; x 2
⇒ Theo định lý Vi-et: 
Khi đó : a.(x – x1).(x – x2)
= a.(x2 – x1.x – x2.x + x1.x2)
= a.x2 – a.x.(x1 + x2) + a.x1.x2
= 
= a . x 2 + b x + c ( đ p c m ) .
* Áp dụng:
a) 2 x 2 – 5 x + 3 = 0
Có a = 2; b = -5; c = 3
⇒ a + b + c = 2 – 5 + 3 = 0
⇒ Phương trình có hai nghiệm 
Vậy: 
b) 3 x 2 + 8 x + 2 = 0
Có a = 3; b' = 4; c = 2
⇒ Δ ’ = 4 2 – 2 . 3 = 10 > 0
⇒ Phương trình có hai nghiệm phân biệt:


* Chứng minh:
Phương trình ax2 + bx + c = 0 có hai nghiệm x1; x2
⇒ Theo định lý Vi-et: 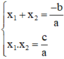
Khi đó : a.(x – x1).(x – x2)
= a.(x2 – x1.x – x2.x + x1.x2)
= a.x2 – a.x.(x1 + x2) + a.x1.x2
= 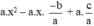
= a.x2 + bx + c (đpcm).
* Áp dụng:
a) 2x2 – 5x + 3 = 0
Có a = 2; b = -5; c = 3
⇒ a + b + c = 2 – 5 + 3 = 0
⇒ Phương trình có hai nghiệm 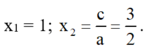
Vậy: