chứng minh rằng trong hình thang mà hai đáy không = , đoạn thẳng nối trung điểm của 2 đường chéo bằng nửa hiệu cạnh đáy
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
6 tháng 7 2018
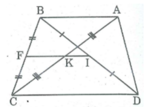
Giả sử hình thang ABCD có AB // CD, AB < CD
Gọi I, K lần lượt là trung điểm hai đường chéo BD, AC; F là trung điểm của BC.
* Trong ∆ ACB, ta có:
K là trung điểm của cạnh AC
F là trung điểm của cạnh BC
Nên KF là đường trung bình của ∆ ACB
⇒ KF // AB và KF = 1/2 AB
(tính chất đường trung bình của tam giác)
Trong ∆ BDC, ta có: I là trung điểm của cạnh BD
F là trung điểm của cạnh BC
Nên IF là đường trung bình của ∆ BDC
⇒ IF // CD và IF = 1/2 CD (tính chất đường trung bình của tam giác)
FK // AB mà AB // CD nên FK // CD
FI // CD (chứng minh trên)
Suy ra hai đường thẳng FI và FK trùng nhau.
⇒ I, K, F thẳng hàng, AB < CD ⇒ FK < FI nên K nằm giữa I và F
IF = IK + KF
⇒ IK = IF – KF = 1/2 CD - 1/2 AB = (CD - AB)/2
28 tháng 4 2017
Xét hình thang ABCD có AB // CD và AB < CD.
Gọi M là trung điểm AB, E là trung điểm của BD, F là trung điểm của AC.
Theo tính chất đường trung bình tam giác, ta có : MF // CD và MF = 1/2 CD (1) ME // AB // CD và ME = 1/2 AB (2) Từ (1) và (2) suy ra M, E, F thẳng hàng (vì qua điểm M chỉ có 1 đường thẳng song song với CD). Vì CD > AB nên MF > ME, hay là E nằm giữa M và F. Ta có: \(EF=MF-ME=\dfrac{1}{2}CD-\dfrac{1}{2}AB=\dfrac{1}{2}\left(CD-AB\right)\) (điều phải chứng minh)
16 tháng 7 2016
Xét tam giác BCD có: - KB = KC (gt)
- MB = MD (gt)
MK là trung bình của BCD.
MK song song và bằng ½ CD
Tương tự như trên ta có:
- HN là trung bình ADC. HN song song và bằng ½ CD.
- HM là trung bình ABD. HM song song và bằng ½ AB.
- KN là trung bình của CAB. KN song song và bằng ½ AB.
H, M, N, K thẳng hàng (tiên đề Ơ – clit)
HK là trung bình của hình thang ABCD (tự chứng minh).
HK = (AB + CD)/2 (t/c)
HM + NK + KM + HN = 2HK.
mà MN = HK – HM – NK
MN = (HM + NK + KM + HN)/2 – HM – NK
= (AB + CD)/2 – AB
= 1/2AB – AB + CD/2
= CD/2 – 1/2AB
= (CD – AB)/2 (đpcm)
6 tháng 7 2016
Vẽ hình thang ABCD, AB song song với CD. Lấy M, N lần lượt là trung điểm của BD và AC. Lấy H và K lần lượt là trung điểm của BC và AD.
Xét tam giác BCD có: - KB = KC ( gt )
- MB = MD ( gt )
MK là trung bình của BCD.
MK song song và bằng 1/2 CD
Tương tự như trên ta có:
- HN là trung bình ADC. HN song song và bằng 1/2 CD.
- HM là trung bình ABD. HM song song và bằng 1/2 AB.
- KN là trung bình của CAB. KN song song và bằng 1/2 AB.
H, M, N, K thẳng hàng ( tiên đề Ơ – clit )
HK là trung bình của hình thang ABCD ( tự chứng minh ).
HK = ( AB + CD ) / 2 ( t/c )
HM + NK + KM + HN = 2HK.
mà MN = HK – HM – NK
MN = (HM + NK + KM + HN)/2 – HM – NK
= (AB + CD)/2 – AB
= 1/2AB – AB + CD/2
= CD/2 – 1/2AB
= (CD – AB)/2 (đpcm)
F
3 tháng 8 2018
Giả sử hình thang ABCD có AB // CD, AB < CD.
I, K lần lượt là trung điểm hai đường chéo BD, AC
Gọi F là trung điểm của BC
Trong tam giác ACB ta có:
K là trung điểm của cạnh AC
F là trung điểm của cạnh BC
Nên KF là đường trung bình của ∆ BDC
⇒ KF // AB và KF=\(\frac{1}{2}\)ABKF=\(\frac{1}{2}\)AB (tính chất đường trung bình của tam giác)
Trong tam giác BDC ta có:
I là trung điểm của cạnh BD
F là trung điểm của cạnh BC
Nên IF là đường trung bình của ∆ BDC
⇒ IF // CD và IF=\(\frac{1}{2}\)CDIF=\(\frac{1}{2}\)CD (tính chất đường trung bình của tam giác)
FK // AB mà AB // CD nên FK // CD
FI // CD (chứng minh trên)
Suy ra hai đường thẳng FI và FA trùng nhau.
⇒ I, K, F thẳng hàng, AB < CD ⇒ FK < FI nên K nằm giữa I và F
IF = IK + KF
\(\eqalign{ & \Rightarrow IK = IF - KF \cr & = {1 \over 2}CD - {1 \over 2}AB = {{CD - AB} \over 2} \cr}\)
3 tháng 8 2018
Ta có hình vẽ ( mang tính tương đối )
Gọi ,M,E,F lần lượt là trung điểm của các đoạn AD ; BD ; AC
Xét \(\Delta ABD\)có M,E lần lượt là trung điểm của AD và BD nên ME là đường trung bình của tam giác ADB
Do đó \(ME//AB;ME=\frac{1}{2}AB\)(1)
Xét \(\Delta ADC\)có M;F lần lưượt là trung điểm của AD;AC nên MF là đường trung bình của tam giác ADC
Do đó \(MF=\frac{DC}{2};MF//DC\)mà \(AB//DC\)(vì tứ giác ABCD là hình thang ) nên \(MF//DC\)(2)
Từ (1) và (2) ta có ba điểm M;E;F thẳng hàng ( theo tiên đề Ơ-clit) và
\(FE=FM-EM=\frac{1}{2}\left(CD-AB\right)\)
Vậy trong hình thang mà 2 đáy không bằng nhau đoạn thẳng nối trung điểm của 2 đường chéo bằng nửa hiệu 2 đáy.
20 tháng 3 2020
Giả sử hình thang ABCD có AB // CD, AB < CD.
I, K lần lượt là trung điểm hai đường chéo BD, AC
Gọi F là trung điểm của BC
Trong tam giác ACB ta có:
K là trung điểm của cạnh AC
F là trung điểm của cạnh BC
Nên KF là đường trung bình của ∆ BDC
⇒ KF // AB và KF=12ABKF=12AB (tính chất đường trung bình của tam giá
Trong tam giác BDC ta có:
I là trung điểm của cạnh BD
F là trung điểm của cạnh BC
Nên IF là đường trung bình của ∆ BDC
⇒ IF // CD và IF=12CDIF=12CD (tính chất đường trung bình của tam giác)
FK // AB mà AB // CD nên FK // CD
FI // CD (chứng minh trên)
Suy ra hai đường thẳng FI và FA trùng nhau.
⇒ I, K, F thẳng hàng, AB < CD ⇒ FK < FI nên K nằm giữa I và F
IF = IK + KF
\(\eqalign{
& \Rightarrow IK = IF – KF \cr
& = {1 \over 2}CD – {1 \over 2}AB = {{CD – AB} \over 2} \cr} \)