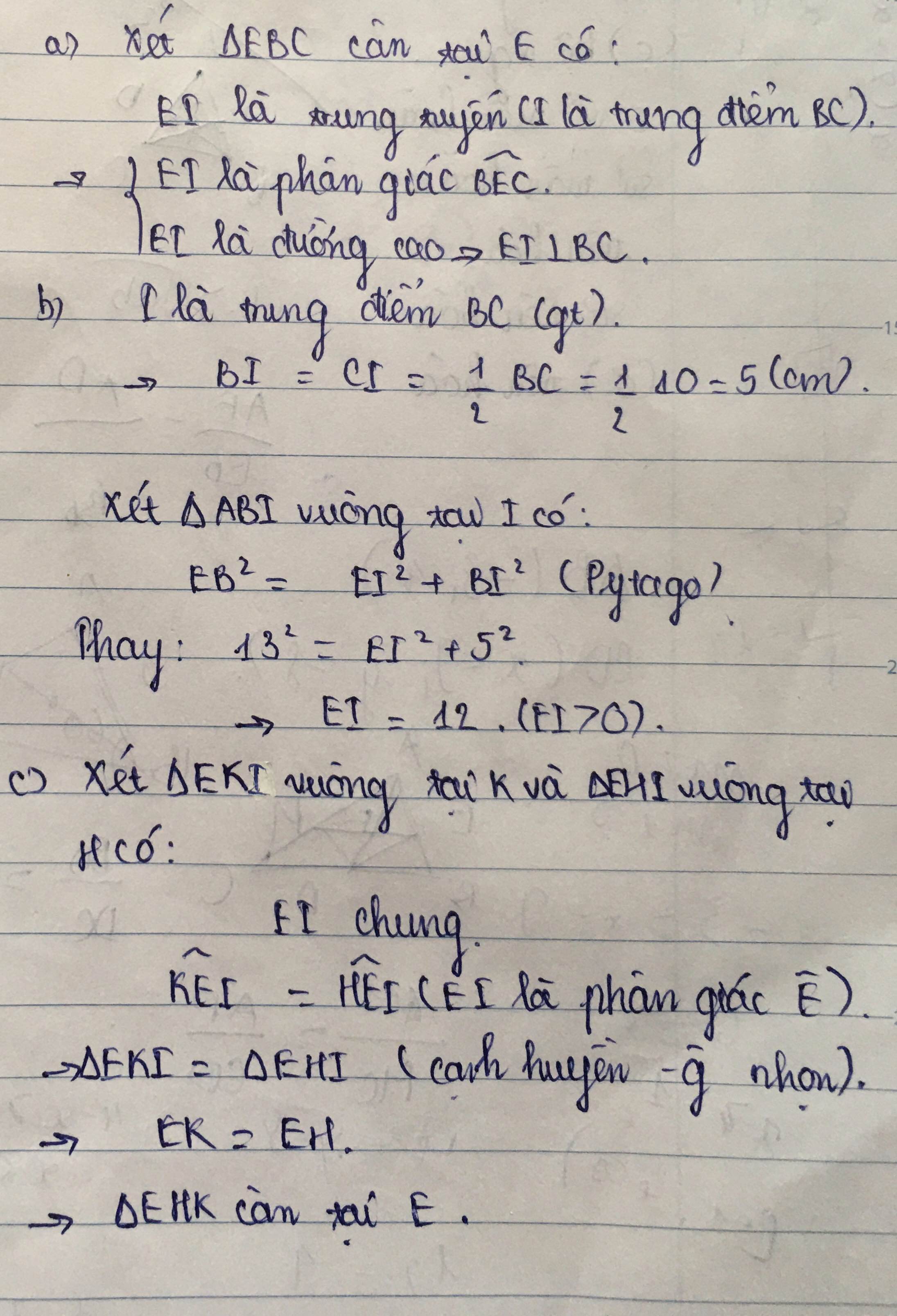Câu 1: Cho tam giác ABC vuông tai A. Kẻ phân giác BD của \(\widehat{ABC}\)( D thuộc AC), trên cạnh BC lấy E sao cho BA = BE.a) Chứng minh tam giác ABD = tam giác EBD và DE vuông góc với BC.b) Giả sử AD= 6cm, DC = 10cm. Tính độ dài đoạn EC.c) Biết tia ED cắt tia BA tại F và gọi M là trung điểm của đoạn FC. Chứng minh ba điểm B,D,M thẳng hàng.Câu 2: Cho tam giác ABC vuông tại A, có Ab = 6cm ; BC = 10cm.a) Tính ACb) Kẻ BD là...
Đọc tiếp
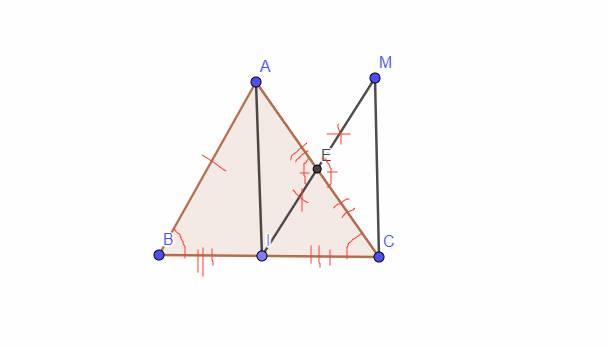
Câu 1: Cho tam giác ABC vuông tai A. Kẻ phân giác BD của \(\widehat{ABC}\)( D thuộc AC), trên cạnh BC lấy E sao cho BA = BE.
a) Chứng minh tam giác ABD = tam giác EBD và DE vuông góc với BC.
b) Giả sử AD= 6cm, DC = 10cm. Tính độ dài đoạn EC.
c) Biết tia ED cắt tia BA tại F và gọi M là trung điểm của đoạn FC. Chứng minh ba điểm B,D,M thẳng hàng.
Câu 2: Cho tam giác ABC vuông tại A, có Ab = 6cm ; BC = 10cm.
a) Tính AC
b) Kẻ BD là phân giác của \(\widehat{ABC}\) (D thuộc AC), kẻ DE vuông góc với BC ( E thuộc BC). Chứng minh DA = DE.
c) Chứng minh BD đi qua trung điểm của AE.
Câu 3: Cho góc xOy ( \(\widehat{xOy}\)không bằng 180o ) và tia Om là phân giác cuẩ góc xOy. Lấy điểm A thuộc Ox ; B thuộc Oy sao cho OA = OB. Gọi I là giao điểm của Om và AB.
a) Chứng minh tam giác AOI = tam giác BOI
b) Từ I kẻ IE thuộc Ox ( E thuộc Ox ) ; IF vuông góc với Oy ( F thuộc Oy ). Chứng minh tam giác EIF cân.
c) Lấy M trên Ox ( A nằm giữa O và M ) vẽ MN // Ab ( N thuộc Oy ), gọi H là trung điểm của MN =. Chứng minh 3 điểm O, I, H thẳng hàng.
LÀm ơn giúp với mai mình thi rồi. Vẽ cả hình nhé. Cảm ơn ~