cho tam giác ABC cân tại B kẻ BH vuông góc với AC ( H thộc AC)
a/ chứng minh :HA = HC
b/kẻ HD vuông góc AB ( D thuộc AB), HE vuông góc BC ( E thuộc BC) chứng minh HD=HE
c/ chứng min tam giác AED là tam giác cân
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1 tháng 8 2023
Sửa đề: ΔABC có AB=AC
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
=>ΔAHB=ΔAHC
=>HB=HC
b: Xét ΔBDH vuông tại D và ΔCEH vuông tại E có
BH=CH
góc B=góc C
=>ΔBDH=ΔCEH
=>HD=HE
9 tháng 2 2021
a) Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC(ΔABC cân tại A)
AH chung
Do đó: ΔABH=ΔACH(cạnh huyền-cạnh góc vuông)
⇔BH=CH(hai cạnh tương ứng)
b) Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(BH^2+AH^2=AB^2\)
\(\Leftrightarrow BH^2=AB^2-AH^2=5^2-4^2=9\)
hay BH=3(cm)
Vậy: BH=3cm
c) Ta có: ΔABH=ΔACH(cmt)
nên \(\widehat{BAH}=\widehat{CAH}\)(hai góc tương ứng)
hay \(\widehat{DAH}=\widehat{EAH}\)
Xét ΔDAH vuông tại D và ΔEAH vuông tại E có
AH chung
\(\widehat{DAH}=\widehat{EAH}\)(cmt)
Do đó: ΔDAH=ΔEAH(cạnh huyền-góc nhọn)
Suy ra: AD=AE(hai cạnh tương ứng)
Xét ΔADE có AD=AE(cmt)
nên ΔADE cân tại A(Định nghĩa tam giác cân)
KB
9 tháng 5 2021
a) Chứng minh HB=HC: Xét ΔAHB và ΔAHC có: ∠AHB=∠AHC=90(độ) AH cạnh chung AB=AC(gt) ⇒ ΔAHB = ΔAHC (ch-cgv) ⇒ HB=HC (2 cạnh tương ứng)
b) Ta có: HB=HC=BC/2=6/2=3(cm) Ta có: ΔAHB vuông tại H. ⇒ AH(mũ 2)+BH(mũ 2)=AB(mũ 2) ⇒ AH(mũ 2)=AB(mũ 2)-BH(mũ 2) =4(mũ 2)-3(mũ 2)=16-9=7 ⇒ AH=√7(cm)
c) Ta có: ΔAHB = ΔAHC ⇒ ∠BAH=∠CAH Xét ΔAHD và ΔAHE có: ∠D=∠E=90(độ) AH cạnh chung ∠BAH=∠CAH (gt) ⇒ ΔAHD = ΔAHE (ch-gn) ⇒ DH=EH ⇒ ΔHDE cân tại H.
25 tháng 12 2020
a) ta có AH⊥BC \(\Rightarrow\)\(\widehat{AHB}=\widehat{AHC}\)=90 độ
ta có AB=AC \(\Rightarrow\)\(\Delta\)ABC cân tại A
\(\Rightarrow\)\(\widehat{ABC}\)=\(\widehat{ACB}\) hay\(\widehat{ABH}=\widehat{ACH}\)
Xét \(\Delta\)AHB\(\left(\widehat{AHB}=90độ\right)\) và \(\Delta\)AHC \(\left(\widehat{AHC}=90\right)độ\) có
AB=AC(giả thiết)
\(\widehat{ABH}=\widehat{ACH}\) (chứng minh trên)
\(\Rightarrow\) \(\Delta\)AHB= \(\Delta\)AHC(cạnh huyền - góc nhọn)
\(\Rightarrow\)HB=HC(2 góc tương ứng)
vậy HB=HC
b) \(\Delta\)AHB= \(\Delta\)AHC(chứng minh câu a)
\(\Rightarrow\widehat{HAB}=\widehat{HAC}\) hay \(\widehat{HAD}=\widehat{HAE}\)
ta có HD⊥AB \(\Rightarrow\widehat{HDA}=90độ\)
HE⊥AC \(\Rightarrow\widehat{HEA}=90độ\)
Xét \(\Delta\)AHD (\(\widehat{HDA}=90độ\)) và \(\Delta\)AHE \(\left(\widehat{HEA}=90\right)độ\) có
\(\widehat{HAD}=\widehat{HAE}\) (chứng minh trên )
AH là cạnh huyền chung
\(\Rightarrow\)\(\Delta\)AHD = \(\Delta\)AHE (cạnh huyền -góc nhọn)
\(\Rightarrow HD=HE\) ( 2 góc tương ứng)
vậy HD=HE
c) ta có HD⊥AB \(\Rightarrow\widehat{HDB}=90độ\)
HE⊥AC \(\Rightarrow\widehat{HEC}=90độ\)
\(\Delta\)ABC cân tại A \(\Rightarrow\widehat{ABC}=\widehat{ACB}\) hay \(\widehat{DBH}=\widehat{ECH}\)
Xét \(\Delta\)HDB\(\left(\widehat{HDB}=90độ\right)\) và \(\Delta\)HEC \(\left(\widehat{HEC}=90độ\right)\)
BH=HC (chứng minh câu a)
\(\widehat{DBH}=\widehat{ECH}\) (chứng minh trên)
\(\Rightarrow\Delta HDB=\Delta HEC\) (cạnh huyền -góc nhọn)
\(\Rightarrow BD=EC\) (2 cạnh tương ứng )
vậy BD =EC
TC
Thầy Cao Đô
Giáo viên
VIP
27 tháng 12 2022
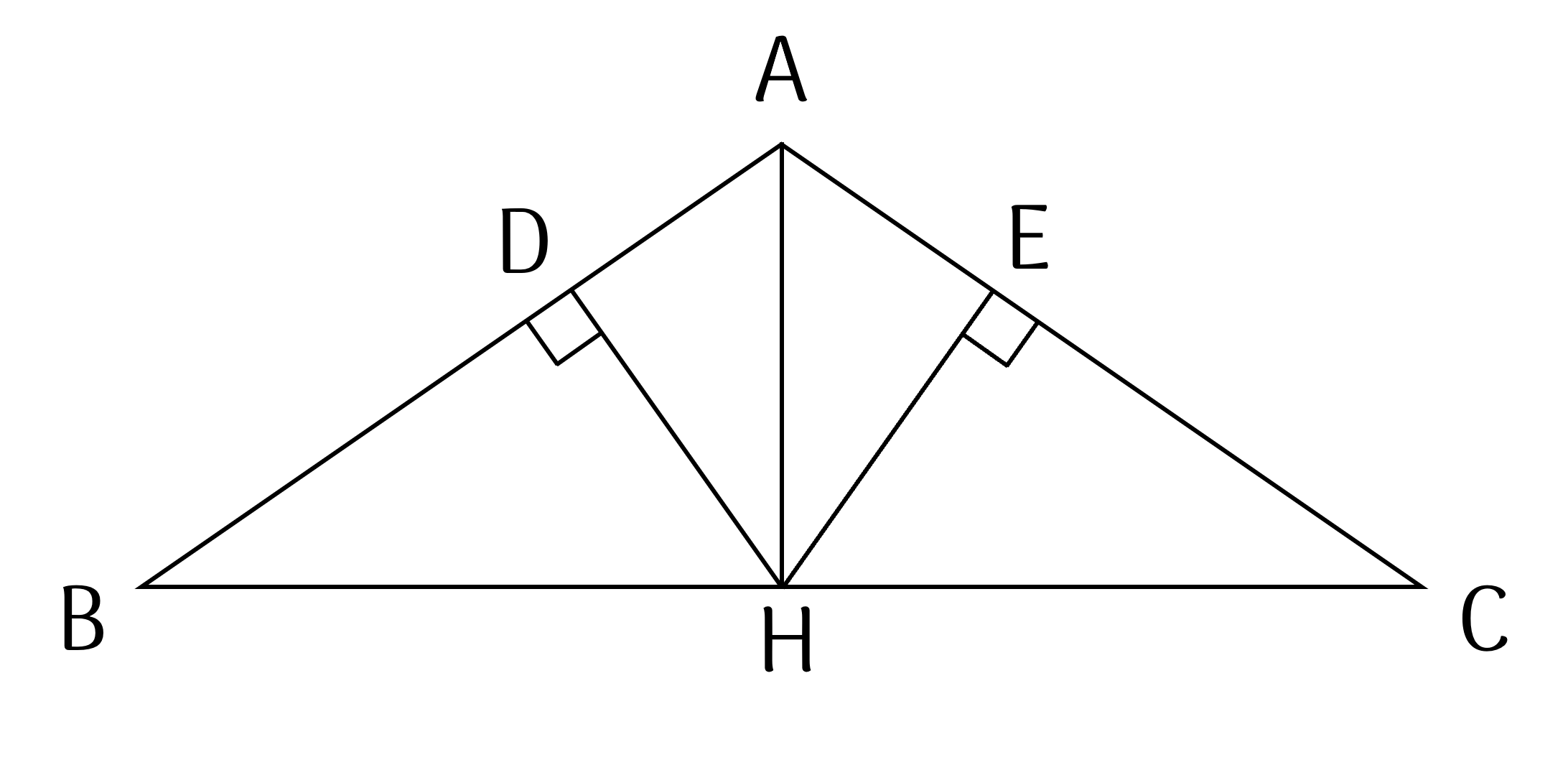
a) Xét hai tam giác vuông $AHB$ và $AHC$ có:
$AH$ là cạnh chung;
$AB = AC$ (gt);
Suy ra $\Delta AHB=\Delta AHC$ (cạnh huyền - cạnh góc vuông)
Suy ra $HB = HC$ (Hai cạnh tương ứng)
$\widehat{BAH} = \widehat{CAH}$ (hai góc tương ứng).
b) Xét hai tam giác vuông $ADH$ và $AEH$ có:
$AH$ là cạnh chung;
$\widehat{BAH} = \widehat{CAH}$ (cmt);
Suy ra $\Delta ADH=\Delta AEH$ (cạnh huyền - góc nhọn).
Suy ra $HD = HE$ (Hai cạnh tương ứng) nên $\Delta HDE$ cân tại $H$.
13 tháng 7 2023
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
=>ΔAHB=ΔAHC
=>HB=HC
b: BH=CH=12/2=6cm
=>AC=căn AH^2+HC^2=10cm
c: Xét ΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
góc DAH=góc EAH
=>ΔADH=ΔAEH
=>HD=HE
=>ΔHDE cân tại H
23 tháng 6 2022
a: Ta có: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểmcủa BC
hay HB=HC
b: Xét ΔADH vuông tạiD và ΔAEH vuông tại E có
AH chung
\(\widehat{DAH}=\widehat{EAH}\)
Do đó: ΔADH=ΔAEH
Suy ra HD=HE
hay ΔHDE cân tại H