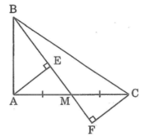
Cho tam giác ABC vuông tại A, M là trung điểm của AC. Gọi E và F là chân các đường vuông góc lần lượt kẻ từ A và C đến đường thẳng BM.
a )Chứng minh ME = MF?
b)So sánh AB và BE + BF/ 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

chín phần hai mươi đề xi mét khối băng bao nhiêu xăng ti mét khối
Vì sao?

Trong ΔABM, ta có ∠(BAM) = 90o
Suy ra: AB < BM (trong tam giác vuông cạnh huyền lớn nhất)
Mà BM = BE + EM = BF - MF
Suy ra: AB < BE + EM
AB < BF - FM
Suy ra:AB + AB < BE + ME + BF - MF (1)
Xét hai tam giác vuông AEM và CFM, ta có:
∠(AEM) = ∠(CFM) = 90o
AM = CM (gt)
∠(AME) = ∠(CMF) (đối đỉnh)
Suy ra: ΔAEM = ΔCFM (cạnh huyền - góc nhọn)
Suy ra: ME = MF (2)
Từ (1) và (2) suy ra: AB + AB < BE + BF
Suy ra: 2AB < BE + BF
Vậy AB < (BE + BF) / 2 .

định lý thường nói : nếu trong 1 tam giác có tông độ dài hai cạnh luôn luôn lớn hơn cạnh còn lại
bạn dựa vào định lý đó để chứng minh
thanks

a: Xét ΔMEA vuông tại E và ΔMFC vuông tại F có
MA=MC
góc AME=góc CMF
=>ΔMEA=ΔMFC
=>ME=MF
b: BE+BF
=BE+BE+EF
=BE+BE+2*ME
=2*BE+2*ME
=2*BM
c: ΔAMB vuông tại A
=>AB<BM

a, Xét △MEA vuông tại E và △MFC vuông tại F
Có: MA = MC (gt)
EMA = FMC (2 góc đối đỉnh)
=> △MEA = △MFC (ch-gn)
=> ME = MF (2 cạnh tương ứng)
b, Ta có: BE = BM - ME và BF = BM + MF
=> BE + BF = BM - ME + BM + MF
=> BE + BF = (BM + BM) - (ME - MF)
=> BE + BF= 2BM
c, Xét △ABM vuông tại A có: AB < BM (quan hệ cạnh)
d, Ta có: BE + BF = 2BM
=> (BE + BF) : 2 = BM
Lại có: AB < BM (cmt)
=> AB < (BE + BF) : 2

a: Xét ΔAME vuông tại E và ΔCMF vuông tại F có
MA=MC
góc AME=góc CMF
=>ΔAME=ΔCMF
b: BE+BF=2BE+EF
=2BE+2ME
=2BM>2BA
=>AB<(BE+BF)/2