cho tam giác ABC có phân giác AM.biết AB = 24 cm , AC = 32 cm , BC = 35 cm . khi đó độ dài y trong hình là A.20 cm B.18 cm C.10 cm D12 cm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 9 2023
a: Xét ΔCAB có CA^2+CB^2=AB^2
nên ΔCAB vuông tại C
Xét ΔCAB vuông tại C có CH là đường cao
nên CH*AB=CA*CB
=>CH*25=15*20=300
=>CH=12(cm)
b: góc BCD+góc ACD=90 độ
góc BDC+góc HCD=90 độ
mà góc ACD=góc HCD
nên góc BCD=góc BDC
=>ΔBDC cân tại B
c: BC^2+BD^2+CD^2
=BC^2+BC^2+CD^2
=2BC^2+CD^2
=2(BH^2+HC^2)+CH^2+HD^2
=2BH^2+3CH^2+DH^2
TH
5 tháng 9 2023
Trong △ABC, ta có: AD là đường phân giác của (BAC)
Suy ra: 
(tính chất đường phân giác)
Mà AB = 15 (cm); AC = 20 (cm)
Nên 
Suy ra: 
(tính chất tỉ lệ thức)
Suy ra: 
LN
Lưu Nguyễn Hà An
CTVHS
4 tháng 9 2023
Trong △ABC, ta có: AD là đường phân giác của (BAC)
Suy ra: (tính chất đường phân giác)
Mà AB = 15 (cm); AC = 20 (cm)
Nên
Suy ra: (tính chất tỉ lệ thức)
Suy ra:
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 4 2023
Đặt \(\left\{{}\begin{matrix}BD=x\\CD=y\end{matrix}\right.\) với x;y là các số nguyên dương
Áp dụng định lý phân giác:
\(\dfrac{BD}{AB}=\dfrac{CD}{AC}\Rightarrow\dfrac{x}{35}=\dfrac{y}{50}\Rightarrow y=\dfrac{10x}{7}\)
Do \(y\) nguyên và 10;7 nguyên tố cùng nhau \(\Rightarrow x\) chia hết cho7
Mặt khác theo BĐT tam giác:
\(BC< AB+AC\Rightarrow x+y< 85\)
\(\Rightarrow x+\dfrac{10x}{7}< 85\Rightarrow x< 35\)
BC lớn nhất khi x lớn nhất, số nguyên chia hết cho 7 và nhỏ hơn 35 lớn nhất là 28
Vậy \(x_{max}=28\Rightarrow BC_{max}=28+\dfrac{10.28}{7}=68\)
27 tháng 11 2017
Tổng độ dài AB và AC là 120 - 50 = 70 (cm)
Độ dài AB là (70 - 10) : 2 = 30 (cm)
Độ dài AC là (70 + 10) : 2 = 40 (cm)
Diện tích tam giác ABC là 30 x 40 : 2 = 600 (cm2)
Chiều cao hạ từ A xuống cạnh AC là 600 : 50 = 12 (cm)
TT
23 tháng 5 2015
a)
* Ta có: AB + AC + BC = 120 (cm)
Suy ra: AB + AC + 50 (cm) = 120 (cm)
Suy ra: AB + AC = 120 (cm) - 50 (cm)
Suy ra: AB + AC = 70 (cm)
* Mà độ dài cạnh AC lớn hơn AB 10 cm (gt)
* Nên:
AB = ( 70 - 10 ) : 2 = 60 : 2 = 30 (cm)
AC = ( 70 + 10 ) : 2 = 80 : 2 = 40 (cm)
Vậy: AB = 30 cm ; AC = 40 cm
b)
* Diện tích hình tam giác ABC là:
( 40 x 30 ) : 2 = 120 : 2 = 60 (cm)
Vậy diện tích tam giác ABC = 60 cm
15 tháng 3 2021
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=18^2+20^2=724\)
hay \(BC=2\sqrt{181}cm\)
Vậy: \(BC=2\sqrt{181}cm\)
5 tháng 2 2022
a: BC=10cm
C=AB+BC+AC=6+8+10=24(cm)
b: Xét ΔABD vuông tại A và ΔHBD vuông tại H có
BD chung
\(\widehat{ABD}=\widehat{HBD}\)
Do đó: ΔABD=ΔHBD
c: Ta có: ΔABD=ΔHBD
nên DA=DH
mà DH<DC
nên DA<DC
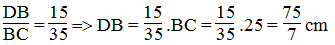
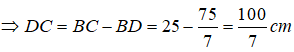
B
B