Giúp mình bài 4,5,6 với ạ. Cảm ơn mọi người trước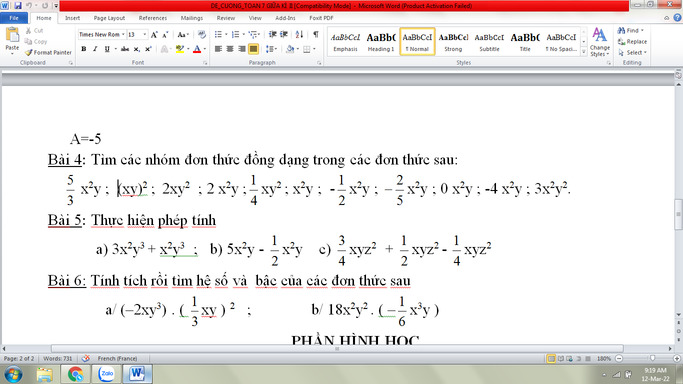 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KA
2
17 tháng 7 2021
Bài 1:
(1) \(4Al+3O_2\xrightarrow[]{t^o}2Al_2O_3\)
(2) \(Al_2O_3+6HCl\rightarrow2AlCl_3+3H_2O\)
(3) \(AlCl_3+3KOH\rightarrow3KCl+Al\left(OH\right)_3\downarrow\)
(4) \(Al\left(OH\right)_3+3HCl\rightarrow AlCl_3+3H_2O\)
(5) \(2Al\left(OH\right)_3\xrightarrow[]{t^o}Al_2O_3+3H_2O\)
(6) \(Al\left(OH\right)_3+NaOH\rightarrow NaAlO_2+2H_2O\)
(7) \(Al_2O_3+2NaOH\rightarrow2NaAlO_2+H_2O\)
(8) \(Al+NaOH+H_2O\rightarrow NaAlO_2+\dfrac{3}{2}H_2\uparrow\)
(9) \(2Al_2O_3\xrightarrow[criolit]{đpnc}4Al+3O_2\)
17 tháng 7 2021
Bài 2:
PTHH: \(Fe+H_2SO_4\rightarrow FeSO_4+H_2\uparrow\)
a_______a_______a_____a (mol)
\(Mg+H_2SO_4\rightarrow MgSO_4+H_2\uparrow\)
b_______b________b____b (mol)
Ta lập HPT: \(\left\{{}\begin{matrix}56a+24b=21,6\\a+b=\dfrac{11,2}{22,4}=0,5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=0,3\\b=0,2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\%m_{Fe}=\dfrac{0,3\cdot56}{21,6}\cdot100\%\approx77,78\%\\\%m_{Mg}=22,22\%\end{matrix}\right.\)
Bảo toàn nguyên tố: \(\left\{{}\begin{matrix}n_{Mg\left(OH\right)_2}=n_{Mg}=0,2\left(mol\right)\\n_{Fe\left(OH\right)_2}=n_{Fe}=0,3\left(mol\right)\end{matrix}\right.\)
\(\Rightarrow m_{kết.tủa}=m_{Fe\left(OH\right)_3}+m_{Mg\left(OH\right)_2}=0,3\cdot107+0,2\cdot56=43,3\left(g\right)\)
Theo các PTHH: \(n_{H_2SO_4\left(p/ứ\right)}=0,5\left(mol\right)\) \(\Rightarrow n_{H_2SO_4\left(ban.đầu\right)}=0,5\cdot120\%=0,6\left(mol\right)\)
\(\Rightarrow m_{ddH_2SO_4}=\dfrac{0,6\cdot98}{10\%}=588\left(g\right)\)
Bảo toàn nguyên tố: \(\left\{{}\begin{matrix}n_{MgO}=n_{Mg}=0,2\left(mol\right)\\n_{Fe_2O_3}=\dfrac{1}{2}n_{Fe}=0,15\left(mol\right)\end{matrix}\right.\)
\(\Rightarrow m_{chất.rắn}=m_{MgO}+m_{Fe_2O_3}=0,2\cdot40+0,15\cdot160=32\left(g\right)\)
NH
1
TK
9 tháng 12 2021
Bài 3:
a, Lực hấp dẫn giữa Trái Đất và Mặt Trăng
\(F_{hd}=G\cdot\dfrac{M_1M_2}{r^2}=6,67\cdot10^{-11}\cdot\dfrac{6\cdot10^{24}\cdot7,2\cdot10^{22}}{\left(3,84\cdot10^8\right)^2}=1,95\cdot10^{20}\left(N\right)\)
NH
1
2 tháng 12 2021
Bài 3.
Định luật ll Niu-tơn:
\(\overrightarrow{F}+\overrightarrow{F_{ms}}=m\cdot\overrightarrow{a}\)
\(\Rightarrow F-F_{ms}=m\cdot a\)
Gia tốc vật:
\(a=\dfrac{F-F_{ms}}{m}=\dfrac{4,5-\mu mg}{m}=\dfrac{4,5-0,2\cdot1,5\cdot10}{1,5}=1\)m/s2
Vận tốc vật sau 2s:
\(v=a\cdot t=1\cdot2=2\)m/s
TK
0
HK
1
6 tháng 12 2021
a: Xét tứ giác MAOB có
\(\widehat{MAO}+\widehat{MBO}=180^0\)
Do đó: MAOB là tứ giác nội tiếp
AH
Akai Haruma
Giáo viên
17 tháng 9 2021
Lời giải:
Đổi $3h15'$ thành $3,25$ giờ
Trong 1 giờ:
Vòi thứ nhất chảy được: $\frac{1}{4,5}$ (bể)
Vòi thứ hai chảy được: $\frac{1}{3,25}$ (bể)
Trong 1 giờ thì cả hai vòi cùng chảy được: $\frac{1}{4,5}+\frac{1}{3,25}=\frac{62}{117}$ (bể)
Hai vòi cùng chảy thì sẽ đầy bể sau:
$1:\frac{62}{117}=\frac{117}{62}$ giờ
Đổi $\frac{117}{62}$ giờ thành $1$ giờ $53$ phút $14$ giây
W
1
12 tháng 10 2021
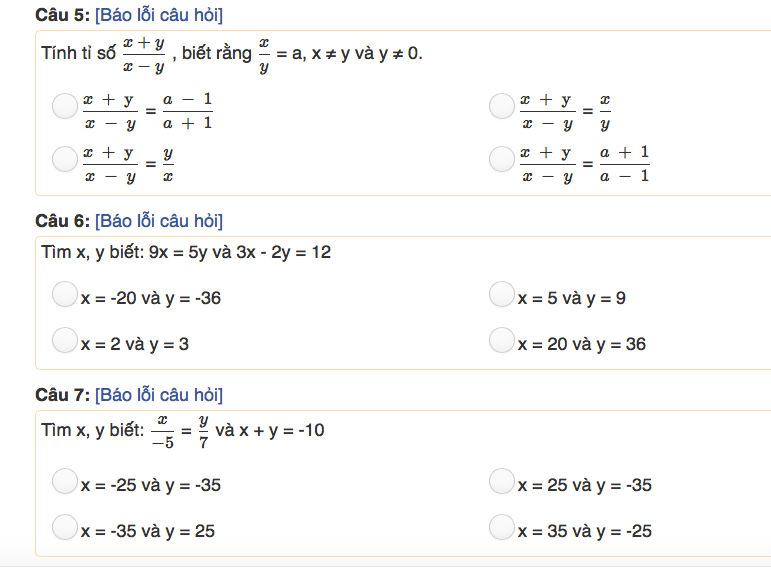
Câu 5:
\(\dfrac{x}{y}=a\Rightarrow\dfrac{x}{a}=\dfrac{y}{1}=\dfrac{x-y}{a-1}=\dfrac{x+y}{a+1}\)
\(\Rightarrow\dfrac{x+y}{x-y}=\dfrac{a+1}{a-1}\)
Câu 6:
\(9x=5y\Rightarrow\dfrac{x}{5}=\dfrac{y}{9}\)
\(\Rightarrow\dfrac{x}{5}=\dfrac{y}{9}=\dfrac{3x}{15}=\dfrac{2y}{18}=\dfrac{3x-2y}{15-18}=\dfrac{12}{-3}=-4\)
\(\Rightarrow\left\{{}\begin{matrix}x=\left(-4\right).5=-20\\y=\left(-4\right).9=-36\end{matrix}\right.\)
Câu 7:
\(\dfrac{x}{-5}=\dfrac{y}{7}=\dfrac{x+y}{-5+7}=\dfrac{-10}{2}=-5\)
\(\Rightarrow\left\{{}\begin{matrix}x=\left(-5\right).\left(-5\right)=25\\y=\left(-5\right).7=-35\end{matrix}\right.\)
AH
Akai Haruma
Giáo viên
27 tháng 6 2021
Bài 5:
\(y=m\sqrt{x^2-4x+7}-(3x-4)=\frac{(m^2-9)x^2+(24-4m^2)x+(7m^2-16)}{m\sqrt{x^2-4x+7}+3x-4}\)
Để đths $y$ có TCN thì:\(\lim\limits_{x\to \pm \infty}y\) hữu hạn
Để điều này xảy ra thì $m^2-9=0\Leftrightarrow m=\pm 3$
Kiểm tra lại thấy cả 2 giá trị này đều thỏa mãn.
AH
Akai Haruma
Giáo viên
27 tháng 6 2021
Bài 6: Tiệm cận của ĐTHS chứ làm gì có tiệm cận hàm số hả bạn?
a.
\(y=\frac{x^2-3x+2}{2x^2+x-1}=\frac{x^2-3x+2}{(2x-1)(x+1)}\)
$(2x-1)(x+1)=0\Leftrightarrow x=\frac{1}{2}$ hoặc $x=-1$
Do đó TCĐ của ĐTHS là $x=\frac{1}{2}$ và $x=-1$
Mặt khác: \(\lim\limits_{x\to \pm \infty}\frac{x^2-3x+2}{2x^2+x-1}=\frac{1}{2}\) nên $y=\frac{1}{2}$ là TCN của ĐTHS.
b.
$x+1=0\Leftrightarrow x=-1$ nên $x=-1$ là TCĐ của đths
$\lim\limits_{x\to \pm \infty}\frac{1-x}{1+x}=-1$ nên $y=-1$ là TCN của đths
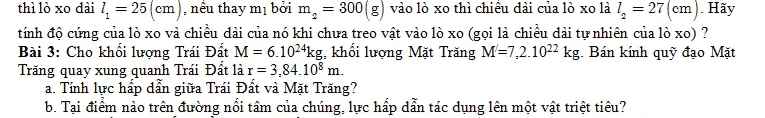
Bài 5:
a: \(=4x^2y^3\)
b: \(=\dfrac{9}{2}x^2y\)
c: \(=xyz^2\left(\dfrac{3}{4}-\dfrac{1}{4}+\dfrac{1}{2}\right)=xyz^2\)
Bài 4
Nhóm 1: \(\dfrac{5}{3}x^2y,2x^2y,x^2y,\dfrac{1}{2}x^2y,\dfrac{-1}{2}x^2y,\dfrac{-2}{5}x^2y,0x^2y,-4x^2y\)
Nhóm 2: \(\left(xy\right)^2,3x^2y^2\)
Bài 5
\(a,3x^2y^3+x^2y^3\)
\(=4x^2y^3\)
\(b,5x^2y-\dfrac{1}{2}x^2y\)
\(=\left(5-\dfrac{1}{2}\right)\left(x^2y\right)\)
\(=\dfrac{9}{2}x^2y\)
\(c,\dfrac{3}{4}xyz^2+\dfrac{1}{2}xyz^2-\dfrac{1}{4}xyz^2\)
\(=\left(\dfrac{3}{4}+\dfrac{1}{2}-\dfrac{1}{4}\right)\left(xyz^2\right)\)
\(=\left(\dfrac{3}{4}+\dfrac{2}{4}-\dfrac{1}{4}\right)\left(xyz^2\right)\)
\(=xyz^2\)
Bài 6
\(a,\left(-2xy^3\right)\left(\dfrac{1}{3}xy\right)^2\)
\(=\left(-2.\dfrac{1}{9}\right)\left(x.x^2\right)\left(y^3y^2\right)\)
\(=\dfrac{-2}{9}x^3y^5\)
Bậc: 3 + 5 = 8
Hệ số: \(\dfrac{-2}{9}\)
\(b,18x^2y^2\left(\dfrac{-1}{6}x^3y\right)\)
\(=\left(-18.\dfrac{1}{6}a\right)\left(x^2x^2\right)\left(y^2y^3\right)\)
\(=-3ax^4y^5\)
Bậc: 4 + 5 = 9
Hệ số: \(-3a\)