Giúp mình câu f,g,f,k với ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 10 2021
\(k,=\dfrac{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)+5\left(\sqrt{a}-\sqrt{b}\right)}{\sqrt{a}+\sqrt{b}+5}\\ =\dfrac{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}+5\right)}{\sqrt{a}+\sqrt{b}+5}=\sqrt{a}-\sqrt{b}\)
8 tháng 10 2021
\(h,=\dfrac{1}{2a-1}\sqrt{25a^2\left(a^2-4a+4\right)}=\dfrac{1}{2a-1}\sqrt{25a^2\left(a-2\right)^2}\\ =\dfrac{\left|5a\left(a-2\right)\right|}{2a-1}=\left[{}\begin{matrix}\dfrac{5a\left(a-2\right)}{2a-1}\left(a\ge2;a\ne\dfrac{1}{2}\right)\\\dfrac{5a\left(2-a\right)}{2a-1}\left(0\le a< 2;a\ne\dfrac{1}{2}\right)\\\dfrac{-5a\left(2-a\right)}{2a-1}\left(a< 0\right)\end{matrix}\right.\)
25 tháng 2 2023
f: 5y^2-20=0
=>y^2-4=0
=>(y-2)(y+2)=0
=>y=2 hoặc y=-2
g: |x-2|-1=0
=>|x-2|=1
=>x-2=1 hoặc x-2=-1
=>x=3 hoặc x=1
26 tháng 9 2021
\(81^7-27^9-9^{13}=\left(3^4\right)^7-\left(3^3\right)^9-\left(3^2\right)^{13}=3^{28}-3^{27}-3^{26}=3^{26}\left(3^2-3-1\right)=3^{24}.3^2.5=3^{24}.45⋮45\)
31 tháng 10 2021
a: \(A=\dfrac{x}{x-4}+\dfrac{\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}+\dfrac{\sqrt{x}-2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}-2}\)
TQ
5
AH
Akai Haruma
Giáo viên
17 tháng 7 2021
Lời giải:
b. Tam giác $ABC$ vuông tại $A$ và $C=45^0$ nên:
$B=90^0-C=90^0-45^0=45^0$
Do đó, tam giác $ABC$ vuông cân tại $A$
$\Rightarrow AC=AB=50$ (cm)
Áp dụng định lý Pitago: $BC=\sqrt{AB^2+AC^2}=\sqrt{50^2+50^2}=50\sqrt{2}$ (cm)
f.
Theo định lý Pitago: $AC=\sqrt{BC^2-AB^2}=\sqrt{7^2-5^2}=2\sqrt{6}$ (cm)
$\sin B=\frac{AC}{BC}=\frac{2\sqrt{6}}{7}$
$\Rightarrow B=44,42^0$
$C=90^0-B=90^0-44,42^0=45,58^0$
17 tháng 7 2021
b) Xét ΔABC vuông tại A có \(\widehat{C}=45^0\)(gt)
nên ΔABC vuông cân tại A(Định nghĩa tam giác vuông cân)
Suy ra: \(\widehat{B}=45^0\) và AC=50(cm)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=50^2+50^2=5000\)
hay \(BC=50\sqrt{2}\left(cm\right)\)
LT
2
18 tháng 9 2021
c) \(=\left(5a-\dfrac{1}{3}\right)^2\)
d) \(=\left(y-\dfrac{1}{3}\right)^2\)
e) \(=\left(2x-y+1\right)^2\)
f) \(=\left(2x-4y\right)^2+2\left(2x-4y\right)+1=\left(2x-4y+1\right)^2\)
g) \(=\left(2xy^2-3\right)^2\)
18 tháng 9 2021
\(c,=\left(5a-\dfrac{1}{3}\right)^2\\ d,=\left(y^4-\dfrac{1}{3}\right)^2\\ e,=\left(2x-y+1\right)^2\\ f,=\left(2x-4y\right)^2+4\left(x-2y\right)+1=\left(2x-4y+1\right)\\ g,=\left(2xy^2-3\right)^2\)
12 tháng 4 2022
a: \(f\left(-2\right)=5\cdot4-8-8=4\)
b: \(f\left(x\right)+g\left(x\right)=6x^2+2x-8\)
c: Đặt G(x)=0
=>x(x-2)=0
=>x=0 hoặc x=2
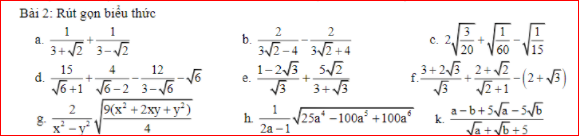
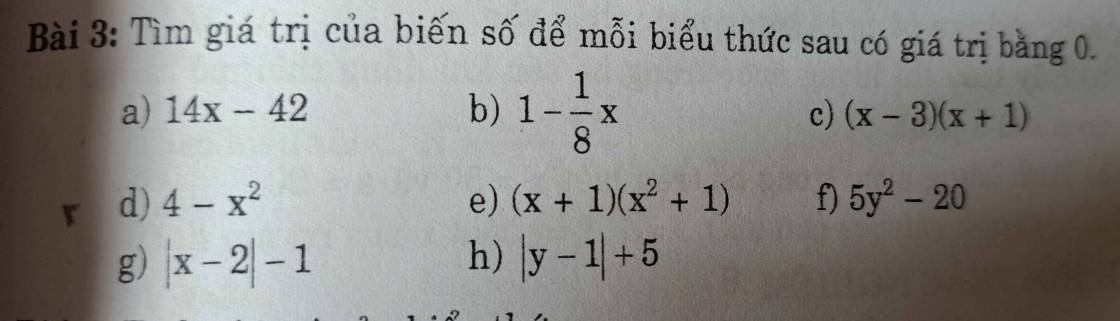
f: Thay x=0 và y=5 vào (d), ta được:
m-1=5
hay m=6
e: Thay x=1 và y=4 vào (d),ta được:
2m+3+m-1=4
=>3m+2=4
hay m=2/3