1.Cho hình lập phương ABCD.EFGH. Hãy tính góc giữa 2 vecto AF và vecto EG
2.Cho hình chóp S.ABCD có tất cả các cạnh đều bằng a. Gọi I và J lần lượt là trung điểm của SC và BC. Số đo của góc (IJ,CD) bằng?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 3 2022
a. Gọi cạnh lập phương là a
Ta có: \(AC=\sqrt{AB^2+AD^2}=a\sqrt{2}\)
\(AH=\sqrt{AD^2+DH^2}=a\sqrt{2}\)
\(CH=\sqrt{CD^2+DH^2}=a\sqrt{2}\)
\(\Rightarrow\Delta ACH\) đều \(\Rightarrow\widehat{CAH}=60^0\)
b.
Do \(B'C||A'D\Rightarrow\) góc giữa A'B và B'C bằng góc giữa A'B và A'D
Tương tự câu a, ta có tam giác A'BD đều \(\Rightarrow\widehat{BA'D}=60^0\)
c.
Do IJ song song SB (đường trung bình), CD song song AB \(\Rightarrow\) góc giữa IJ và CD bằng góc giữa SB và AB
Tam giác SAB đều (các cạnh bằng a) \(\Rightarrow\widehat{SBA}=60^0\)
d.
\(\overrightarrow{EG}=\overrightarrow{AC}\Rightarrow\widehat{\left(\overrightarrow{AF};\overrightarrow{EG}\right)=\widehat{\left(\overrightarrow{AF};\overrightarrow{AC}\right)}=\widehat{FAC}=60^0}\) do tam giác FAC đều
DN
14 tháng 3 2022
Thầy ơi thầy giúp em dạng này với ạ, em sắp thi rồi ạ :'(( https://hoc24.vn/cau-hoi/a-co-bao-nhieu-gia-tri-cua-a-de-limlimits-xrightarrowinftyleftsqrtx2-ax2021-x1righta2b-tim-a-de-ham-so-fxleftbeginmatrixdfracx31x1khixne-13akhix-1end.5243579572507
CM
18 tháng 11 2017
Đáp án C
MN là đường trung bình của tam giác DAS nên MN//SA.
Gọi O là tâm của hình vuông ABCD, vì SA=SC=SB=SD nên
CM
10 tháng 8 2017
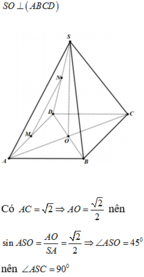
Đáp án C
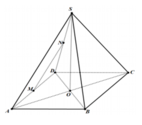
MN là đường trung bình của tam giác DAS nên MN//SA
Gọi O là tâm của hình vuông ABCD, vì SA=SC=SB=SD nên SO ⊥ (ABCD)
CM
17 tháng 6 2018
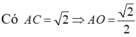
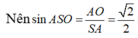
Chứng minh B, J, I thẳng hàng. Áp dụng định lí Mê-nê-la-uýt vào tam giác IAB ta được IJ/JB = 1/4.
Đáp án C
1. Do \(EG||AC\Rightarrow\widehat{\left(\overrightarrow{AF};\overrightarrow{EG}\right)}=\widehat{\left(\overrightarrow{AF};\overrightarrow{AC}\right)}=\widehat{FAC}\)
Mà \(AF=AC=CF=AB\sqrt{2}\Rightarrow\Delta ACF\) đều
\(\Rightarrow\widehat{FAC}=60^0\)
2.
Do I;J lần lượt là trung điểm SC, BC \(\Rightarrow IJ\) là đường trung bình tam giác SBC
\(\Rightarrow IJ||SB\)
Lại có \(CD||BA\Rightarrow\widehat{\left(IJ;CD\right)}=\widehat{SB;BA}=\widehat{SBA}=60^0\) (do các cạnh của chóp bằng nhau nên tam giác SAB đều)