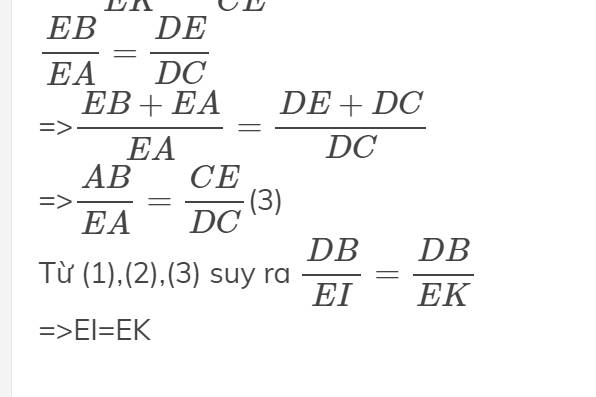Cho tam giác ABC vuông tại A ( AB < AC ) . Kẻ AH vuông góc với BC tại H. Qua B kẻ đường thẳng vuông góc với AB , cắt đường thẳng AH tại D. Gọi tia AB và tia CD cắt nhau tại E. BE DE
a ) Chứng minh : BA DC
b ) Qua E kẻ đường thẳng song song với AC , đường thẳng này lần lượt cắt các đường thăng AD , BC tại I , K. Chứng minh : El = EK ;
c ) Gọi N là giao điểm của EH và AC ; Gọi Q là giao điểm của DN và BC ; Gọi P là giao điểm của BN và AD . Chúng minh : NA = NC và PQ // BD ;
d ) Gọi G là giao điểm của đường thẳng AQ và CD . Qua Q kẻ đường thẳng song song với CE , cắt đường thẳng AC tại T. Chứng minh PT LAD .