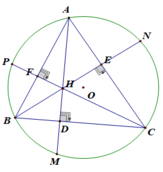
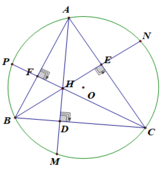
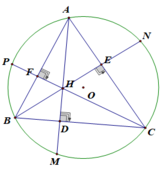
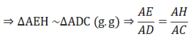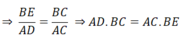Cho tam giác $ABC$ có ba góc nhọn nội tiếp đường tròn $(O)$. Các đường cao $AD$, $BE$, $CF$ cắt nhau tại $H$ và cắt đường tròn $(O)$ lần lượt tại $M$, $N$, $P$. Chứng minh rằng:
a) Tứ giác $AEHF$ nội tiếp.
b) Bốn điểm $B$, $C$, $E$, $F$ cùng thuộc một đường tròn.
c) $AE.AC = AH.AD$ và $AD.BC = BE.AC$.
d) $H$ và $M$ đối xứng nhau qua $BC$.
e) Xác định tâm đường tròn nội tiếp tam giác $DEF$.