Cho đường tròn tâm $O$ đường kính $AB = 2R$. Gọi $C$ là trung điểm của $OA$; qua $C$ kẻ đường thẳng vuông góc với $OA$ cắt đường tròn đó tại hai điểm phân biệt $M$ và $N$. Trên cung nhỏ $BM$ lấy điểm $K$ ($K$ khác $B$ và $M$). Gọi $H$ là giao điểm của $AK$ và $MN$. Chứng minh rằng tứ giác $BCHK$ là tứ giác nội tiếp.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

1 tháng 7 2023
a: góc AKB=1/2*sđ cung AB=90 độ
góc HCB+góc HKB=180 độ
=>HCBK nội tiếp
b: Xét ΔACH vuông tại C và ΔAKB vuông tại K có
góc CAH chung
=>ΔACH đồng dạng với ΔAKB
=>AC/AK=AH/AB
=>AK*AH=AB*AC=2R*1/2R=R^2

30 tháng 6 2023
1: góc MAI+góc MEI=180 độ
=>MAIE nội tiếp
2: góc IEN+góc IBN=180 độ
=>IENB nội tiếp
MAIE nội tiếp
=>góc AMI=góc AEI
IENB nội tiếp
=>góc BIN=góc BEN
góc BEN+góc IEB=90 độ
góc AEI+góc BEI=90 độ
=>góc BEN=góc AEI
=>góc AMI=góc BIN

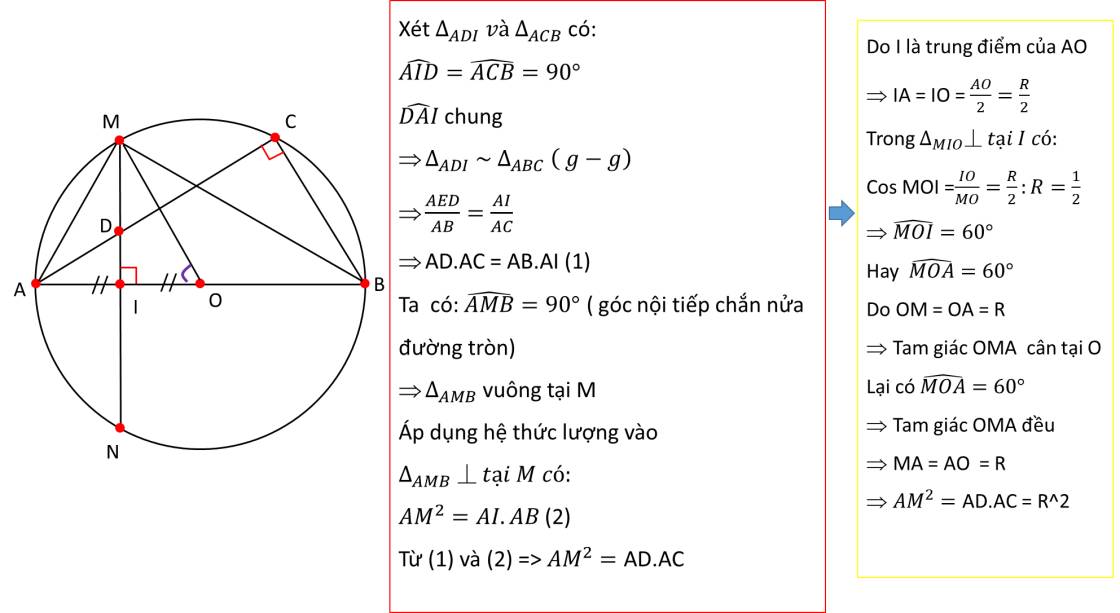
Ta có: góc AKP = 90độ ( Góc nội tiếp chắn nửa đường tròn)
Mà AK giao MN tại H =) Góc HKP = 90độ (1)
Lại có: MC vuông góc AB =) Góc HCB = 90độ (2)
Từ (1) và (2) =) góc HKP + góc HCP = 180độ
Mà 2 góc đối nhau
=) Tứ giác BCHK nội tiếp