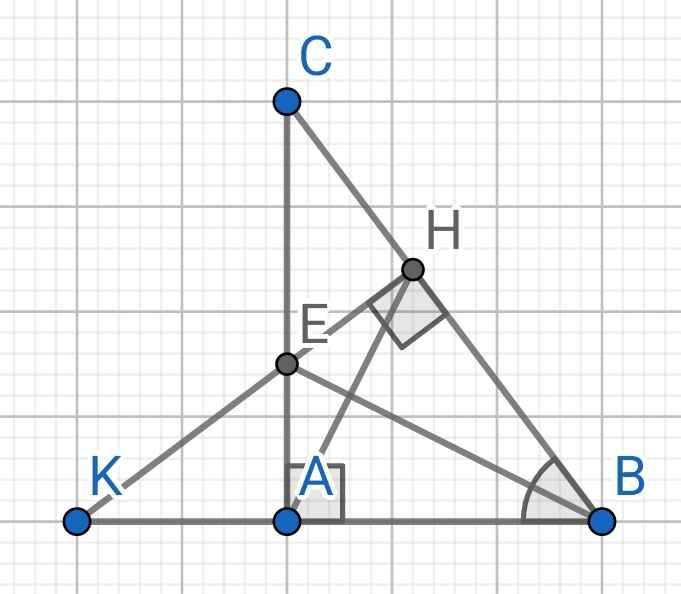
Cho tam giác ABC vuông tại A.Tia phân giác của góc B cắt AC tại E.Kẻ EH vuông góc với BC(H thuộc BC).
1)Chứng minh tam giác ABE= tam giác HBE
2)Chứng minh BE là đường trung trực của AH
3)Trên tia đối của tia AB lấy điểm P sao cho AP=HC
a) Chứng minh PC//AH
b)Chứng minh 3 điểm P,E,H thẳng hàng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABE vuông tại A và ΔHBE vuông tại H có
BE chung
\(\widehat{ABE}=\widehat{HBE}\)
Do đó: ΔABE=ΔHBE
b: ta có: ΔABE=ΔHBE
nên AE=HE; BA=BH
Suy ra: BE là đường trung trực của AH

a: Xét ΔBAE vuông tại A và ΔBDE vuông tại D có
BE chung
góc ABE=góc DBE
=>ΔBAE=ΔBDE
b: BA=BD
EA=ED
=>BE là trung trực của AD
c: góc BAD+góc CAD=90 độ
góc HAD+góc BDA+90 độ
góc BAD=góc BDA
=>góc CAD=góc HAD
=>AD làphân giác của góc HAC

a) Xét ΔABE vuông tại A và ΔHBE vuông tại H có
BE chung
\(\widehat{ABE}=\widehat{HBE}\)(BE là tia phân giác của \(\widehat{ABH}\))
Do đó: ΔABE=ΔHBE(cạnh huyền-góc nhọn)

Bài 1
c) 2.3ˣ.3² = 18
3ˣ⁺² = 18 : 2
3ˣ⁺² = 9
3ˣ⁺² = 3²
x + 2 = 2
x = 2 - 2
x = 0
Bài 2
 a) Do BE là tia phân giác của ∠ABC (gt)
a) Do BE là tia phân giác của ∠ABC (gt)
⇒ ∠ABE = ∠HBE
Xét hai tam giác vuông: ∆ABE và ∆HBE có:
BE là cạnh chung
∠ABE = ∠HBE (cmt)
⇒ ∆ABE = ∆HBE (cạnh huyền - góc nhọn)
b) Gọi D là giao điểm của AH và BE
Do ∆ABE = ∆HBE (cmt)
⇒ AB = HB (hai cạnh tương ứng)
Xét ∆ABD và ∆HBD có:
BD là cạnh chung
∠ABD = ∠HBD (BE là phân giác của ∠ABC)
AB = HB (cmt)
⇒ ∆ABD = ∆HBD (c-g-c)
⇒ AD = HD (hai cạnh tương ứng)
⇒ D là trung điểm của AH (1)
Lại do ∆ABD = ∆HBD (cmt)
⇒ ∠ADB = ∠HDB (hai góc tương ứng)
Mà ∠ADB + ∠HDB = 180⁰ (kề bù)
⇒ ∠ADB = ∠HDB = 180⁰ : 2
= 90⁰ (2)
Từ (1) và (2) ⇒ BD là đường trung trực của AH
Hay BE là đường trung trực của AH
c) Do ∆ABE = ∆HBE (cmt)
⇒ AE = HE (hai cạnh tương ứng)
Xét hai tam giác vuông: ∆AEK và ∆HEC có:
AE = HE (cmt)
∠AEK = ∠HEC (đối đỉnh)
⇒ ∆AEK = ∆HEC (cạnh góc vuông - góc nhọn kề)
⇒ EK = EC (hai cạnh tương ứng)

a: Xét ΔABD vuông tạiA và ΔHBD vuông tại H có
BD chung
góc ABD=góc HBD
=>ΔBAD=ΔBHD
b: BA=BH
DA=DH
=>BD là trung trực của AH
c: Xét ΔDAK và ΔDHC có
DA=DH
góc ADK=góc HDC
DK=DC
=>ΔDAK=ΔDHC
=>góc DAK=góc DHC=90 độ
=>góc DAK+góc DAB=180 độ
=>B,A,K thẳng hàng




1: Xét ΔBAE vuông tại A và ΔBHE vuông tại H có
BE chung
\(\widehat{ABE}=\widehat{HBE}\)
Do đó: ΔBAE=ΔBHE
2: Ta có: ΔBAE=ΔBHE
nên AE=HE;BA=BH
=>BE là đường trung trực của AH
3: Xét ΔBPC có BA/AP=BH/HC
nên AH//PC