Cho một số tự nhiên gồm các số tự nhiên liên tiếp từ 1 đến 1983 được viết theo thứ tự liền nhau như sau:1 2 3 4 5 6 7 8 9 10 11 12 13 .... 1980 1981 1982 1983Hãy tính tổng tất cả các chữ số của số đó.(Giải bằng 3 cách. Bạn nào giải 1 cách cũng được nhưng giải càng nhiều cách càng tốt)(Đề thi học sinh giỏi toàn quốc năm 1983)Đây là dạng toán TÌM TỔNG CÁC SỐ HẠNG CỦA DÃY...
Đọc tiếp
Cho một số tự nhiên gồm các số tự nhiên liên tiếp từ 1 đến 1983 được viết theo thứ tự liền nhau như sau:
1 2 3 4 5 6 7 8 9 10 11 12 13 .... 1980 1981 1982 1983
Hãy tính tổng tất cả các chữ số của số đó.(Giải bằng 3 cách. Bạn nào giải 1 cách cũng được nhưng giải càng nhiều cách càng tốt)
(Đề thi học sinh giỏi toàn quốc năm 1983)
Đây là dạng toán TÌM TỔNG CÁC SỐ HẠNG CỦA DÃY SỐ.
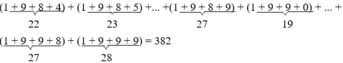
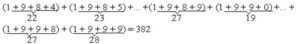
Ta nhận xét:
* các cặp số:
- 0 và 1999 có tổng các chữ số là:
0 + 1 + 9 + 9 + 9 = 28
- 1 và 1998 có tổng các chữ số là:
1 + 1 + 9 + 9 + 8 = 28
- 2 và 1997 có tổng các chữ số là:
2 + 1 + 9 + 9 + 7 = 28
- 998 và 1001 có tổng các chữ số là:
9 + 9 + 8 + 1 + 1 = 28
- 999 và 1000 có tổng các chữ số là:
9 + 9 + 9 + 1 = 28
Như vậy trong dãy số
0, 1, 2, 3, 4, 5,. . . , 1997, 1998, 1999
Hai số hạng cách đều số hạng đầu và số hạng cuối đều có tổng bằng 28. Có 1000 cặp như vậy, do đó tổng các chữ số tạo nên dãy số trên là:
28 x 1000 = 28 000
* Số tự nhiên được tạo thành bằng cách viết liên tiếp các số tự nhiên từ 1984 đến 1999 là * Vậy tổng các chữ số của số tự nhiên đã cho là:
28 000 – 382 = 27 618
Số số hạng của dãy đó là : ( 1983 - 1 ) : 1 + 1 = 1983 ( chữ số )
Tổng của các số hạng đó là : ( 1983 + 1 ) x 1983 : 2 = 1967136
Đáp số 1967136