Trọng tâm , trực tâm và tâm đường tròn ngoại tiếp của tam giác thì thẳng hàng . Hãy chứng minh điều đó .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 4 2016
Cho tam giác ABC có trực tâm H , trọng tâm G , O là tâm đường tròn
ngoại tiếp , I là trung điểm BC , AD là đường kính của (O) .
Chứng minh H , G , O thẳng hàng ?
Giải :
Ta có : góc DCA = góc DBA = 90 độ ( góc nội tiếp chắn 1/2 (O))
Xét tứ giác BHCD ta có :
BH // DC ( vì cùng vuông góc với AC )
CH // DB ( vì cùng vuông góc với AB )
Do đó tứ giác BHCD là hình bình hành .
===> H , I , D thẳng hàng và IH = ID (t/c đường chéo hbhành)
Ta lại có : OI = 1/2 AH ( đ.trung bình tam giác DAH ) (1)
GI = 1/2 GA (t/chất trọng tâm của ABC ) (2)
góc HAG = góc GIO ( so le trong vì AH // OI ) (3)
Do đó tam giác GAH đồng dạng tam giác GIO ( c.g.c)
===> góc HGA = góc IGO (góc tương ứng của 2 t.giác đ.dạng )
Vì góc HGA và góc IGO là 2 góc ở vị trí đối đỉnh bằng nhau nên ta suy ra H , G , O thẳng hàng .
Vậy trong 1 tam giác trực tâm , trọng tâm , tâm đường tròn ngoại tiếp cùng nằm trên 1 đường thẳng đó là đường thẳng Euler !
CM
3 tháng 5 2017
a)
– Tọa độ trọng tâm G của tam giác ABC là:
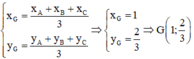
– Tọa độ trực tâm H của tam giác ABC:
Cách 1:
+ Phương trình đường cao BD:
BD ⊥ AC ⇒ Đường thẳng BD nhận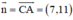 
là một vtpt
BD đi qua B(2; 7)
⇒ Phương trình đường thẳng BD: 7(x - 2) +11(y - 7) = 0 hay 7x + 11y – 91 = 0
+ Phương trình đường cao CE:
CE ⊥ AB ⇒ Đường thẳng CE nhận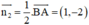 
là một vtpt
CE đi qua C(–3; –8)
⇒ Phương trình đường thẳng CE: 1(x + 3) – 2(y + 8)=0 hay x – 2y – 13 = 0.
Trực tâm H là giao điểm của BD và CE nên tọa độ của H là nghiệm của hpt:
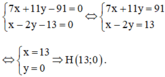
Cách 2: Gọi H(x, y) là trực tâm tam giác ABC
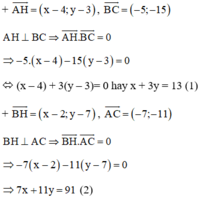
Từ (1) và (2) ta có hệ phương trình
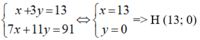
b) Gọi T(x; y) là tâm đường tròn ngoại tiếp tam giác ABC
Khi đó TA = TB = TC = R.
+ TA = TB ⇒ AT2 = BT2
⇒ (x – 4)2 + (y – 3)2 = (x – 2)2 + (y – 7)2
⇒ x2 – 8x + 16 + y2 – 6y + 9 = x2 – 4x + 4 + y2 – 14y + 49
⇒ 4x – 8y = –28
⇒ x – 2y = –7 (1)
+ TB = TC ⇒ TB2 = TC2
⇒ (x – 2)2 + (y – 7)2 = (x + 3)2 + (y + 8)2
⇒ x2 – 4x + 4 + y2 – 14y + 49 = x2 + 6x + 9 + y2 + 16y + 64
⇒ 10x + 30y = –20
⇒ x + 3y = –2 (2)
Từ (1) và (2) ⇒ x = –5, y = 1 ⇒ T(–5 ; 1).
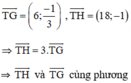
⇒ T, H, G thẳng hàng.
c) Tâm đường tròn ngoại tiếp ΔABC: T(–5; 1)
Bán kính đường tròn ngoại tiếp ΔABC:
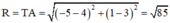
Vậy phương trình đường tròn ngoại tiếp tam giác ABC:
(x + 5)2 + (y – 1)2 = 85
LN
31 tháng 3 2019
https://olm.vn/hoi-dap/detail/215867258818.html bài này mik giải rồi
10 tháng 2 2018
Mình làm theo cách này hơi dài. Mình có đặt thêm điểm và tạo nhiều hình để làm. Có gì sai sót thông cảm nhé
Cho tam giác ABC nhọn có M,N lần lượt là trung điểm BC và AC. Đường thằng vuông góc với AB kẻ từ B và đường thăng vuông góc với AC kẻ từ C cắt nhau tại D. Gọi H là trực tâm, G là trọng tâm, O là tâm đường tròn ngoại tiếp tam giác ABC
Giải:
Bạn là CTV nên mình chỉ ghi ý chính thôi
Chứng minh H,M,D thẳng hàng và MH=MD
Do G là trọng tâm tam giác ABC nên
\(\frac{AG}{AM}=\frac{2}{3}\)
M là trung điểm HD
Nên G cũng là trọng tâm tam giác AHD (*)
Xét tam giác ACD có NA=ND
NO//CD
=> O là trung điểm AD
=> HO là trung tuyếntam giác AHD(**)
Từ (*) và (**) => H,G,O thẳng hàng
11 tháng 5 2016
-Trọng tâm tam giác là giao điểm ba đường trung tuyến
-Trực tâm tam giác là giao điểm bà đường cao kẻ từ 3 đỉnh tam giác
-Giao điểm ba đường trung trực của tam giác là tâm của đường tròn NGOẠI TIẾP
-Giao điểm ba đường phân giác trong của tam giác là tâm đường tròng NỘI TIẾP
Còn các hệ thức trong tam giác vuông mình wên rồi, để bạn nào HS lớp 9 trả
TP
17 tháng 4 2022
bài này giải đc cách lớp 7
chứng minh định lý phụ : đường trung bình (đường nối bởi 2 điểm trung điểm của cạnh 1 và 2 của 1 tam giác) song song với cạnh còn lại
các bạn tự chứng minh định lý phụ kia, định lý này trên mạng có nhiều (có cách giải lớp 7) nên mình sẽ ko chứng minh lại nữa
ta áp dụng định lý phụ vào bài:
vì tâm đường tròn tam giác ngoại tiếp là o => o là giao điểm 3 đường trung trực.
đường thẳng GO cắt AH tại H', F,P,D lần lượt là trung điểm của AG,H'G,BG nên
FP,PD lần lượt là đường trung bình của tam giác BGH', AGH'
=> FP//AH', PD//BH'
vì AH là đường cao, OK là đường trung trực , H' thuộc AH=> AH'//OK
mà FP//AH' => FP//OK
vì AK là đường trung tuyến, trọng tâm G => AG=2GK mà Flà trung điểm của AG => FG=GK
xét tam giác FGP,GOK:
FG=GK, góc OGK=FGP (đối đ), góc GFB=GKO ( FP//OK)
=> OG=GP
vì BM là đường trung tuyến, trộng tâm G, D là trung điểm của BG=> DG=GM
xét tam giác PGD,MOG:
OG=GP, DG=GM, góc G1=G2 (đđ)
=> PD//OM mà PD//BH' => BH'//OM mà OM là đường trung trực => BH' là đường cao mà AH' cũng là đường cao => H' là trực tâm=> H trùng với H' => H,G,O thằng hàng
T
10 tháng 8 2016
Bài này là chứng minh đường thẳng ơ le.
cách 1:
Gọi E,FE,F lần lượt là trung điểm của BC,AC. Ta có EF là đường trung bình của tam giác ABC nên EF//AB.
Ta lại có OF//BH(cùng vuông góc với ACA). Do đó : ˆOFE=ˆABH
Tương tự ˆOEF=ˆBAH
Từ đó ta có tam giác ABH đồng dạng với tam giác EFO
Suy ra AH/OE=AB/EF=2
mà AG/GE=2.
Do đó: AG/EG=AH/OE=2
mà ˆHAG=ˆOEG
⇒ΔHAG∼ΔEOG⇒ˆHGA=ˆEGO
nên ˆHGA+ˆAGO=ˆHGO=180
Vậy H,G,O thẳng hàng.
C2 : dùng véc tơ để tính
C3: dựng đường tròn 9 điểm => ...
10 tháng 8 2016
Ta có : góc DCA = góc DBA = 90 độ ( góc nội tiếp chắn \(\frac{1}{2}\) (O))
Xét tứ giác \(BHCD,\) ta có : \(BH\) // \(DC\) ( vì cùng vuông góc với \(AC\))
\(CH\)// \(DB\) ( vì cùng vuông góc với AB )
Do đó tứ giác \(BHCD\) là hình bình hành .
\(\Rightarrow\) \(H,\)\(I,\)\(D\) thẳng hàng và \(IH=ID\) (tính chất đường chéo hình bình hành)
Ta lại có : \(OI=\frac{1}{2}AH\) ( đường trung bình tam giác \(DAH\) ) \(\left(1\right)\)
\(GI=\frac{1}{2}GA\) (tính chất trọng tâm của \(ABC\) ) \(\left(2\right)\)
Góc\(HAG\) = góc \(GIO\) ( so le trong vì \(AH\) // \(OI\) ) \(\left(3\right)\)
Do đó tam giác \(GAH\) đồng dạng tam giác \(GIO\) ( c.g.c)
\(\Rightarrow\) góc \(HGA\) = góc \(IGO\) (góc tương ứng của 2 tam giác đồng dạng )
Vì góc \(HGA\) và góc \(IGO\) là 2 góc ở vị trí đối đỉnh bằng nhau nên ta suy ra \(H,\) \(G,\)\(O,\)thẳng hàng .
Vậy trong 1 tam giác trực tâm, trọng tâm, tâm đường tròn ngoại tiếp cùng nằm trên 1 đường thẳng đó là đường thẳng Euler !
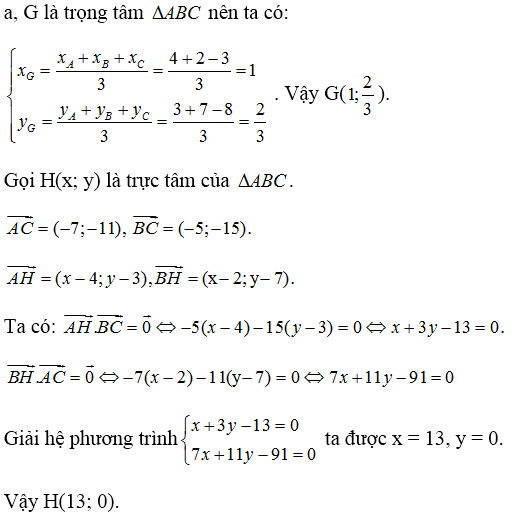
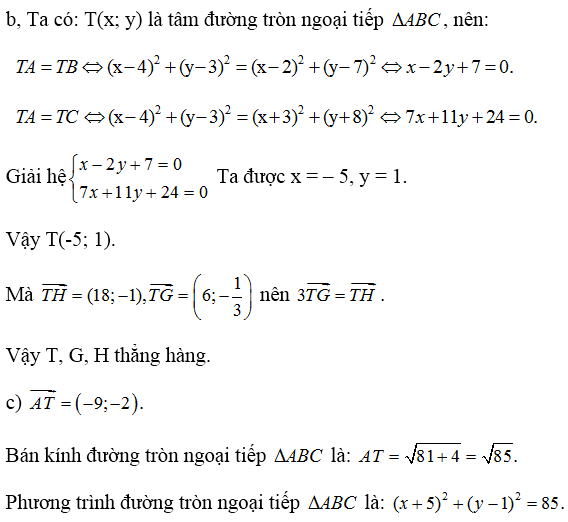
bn xem thử nhé!!
chứng minh bài này có nhiều cách
sau đây là một cách khá đơn giản (theo mình)
xét trong △ABC có H,O lần lượt là trực tâm, tâm đường tròn ngoại tiếp của tam giác.
gọi M là trung điểm của BC
kẻ đường kính BK của (O)
=>tam giác KCB = 90⁰
=>KC⊥BC
H là trực tâm của △ABC
=>AH⊥BC
=>AH//KC
tương tự AK//HC
=>AHCK là hình bình hành
=>AH=KC
△BKC có O,M là trung điểm BK,BC
=>OM là đường trung bình của △
=>OM=KC/2
=>OM=AH/2
gọi G là giao điểm AM và HO
△AHG ∽ △MOG (gg)
=>AH/OM=AG/GM
hay AG/GM=2
AM là trung tuyến của △ABC
=> G là trọng tâm △ABC
=> trong một tam giác trọng tâm, trực tâm, tâm đường tròn ngoại tiếp cùng nằm trên một đường thẳng
đúng thì t i c k nhé!! 45465465767568
Ẹc ẹc mới học xong thi bay hết chữ rùi bạn ơi. Bài này hồi mình có giải trong vbt toán để mk lật xem lại