Đặt vật AB vuông góc với trục chính của TKHT có tiêu cự 20cm, điểm A nằm trên trục chính, cách TK 10 cm. Hãy xác định vị trí, tính chất của ảnh? (ảnh thật hay ảnh ảo, cùng chiều hay ngược chiều với vật, lớn hơn hay nhỏ hơn vật, cách thấu kính một đoạn bằng bao nhiêu...
Đọc tiếp
Đặt vật AB vuông góc với trục chính của TKHT có tiêu cự 20cm, điểm A nằm trên trục chính, cách TK 10 cm. Hãy xác định vị trí, tính chất của ảnh? (ảnh thật hay ảnh ảo, cùng chiều hay ngược chiều với vật, lớn hơn hay nhỏ hơn vật, cách thấu kính một đoạn bằng bao nhiêu cm?)
Tham khảo:
Ảnh thật, ngược chiều, lớn hơn vật và cách thấu kính một khoảng 60cm.
Lời giải:
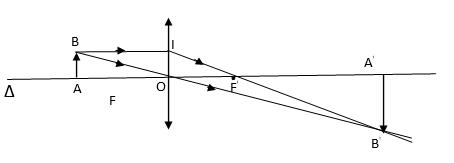
giải tính chiều cao:
ΔOAB ∼ ΔOA'B'
=> \(\dfrac{OA}{OA'}=\dfrac{AB}{A'B'}\left(1\right)\)
ta lại có :
Δ OIF ∼ Δ A'B'F'
=> \(\dfrac{OI}{A'B'}=\dfrac{OF'}{A'B'}\left(2\right)\)
Từ (1) và (2) suy ra : \(\dfrac{OA}{OA'}=\dfrac{OF'}{A'F'}\left(3\right)\)
mà : A'F' = OA' - OF ' (4)
thay số vào (3) và (4) ta được : OA' = 60cm