giúp mình gấp! nhanh nha bạn, mình cần ngay bây giờ, các bạn làm dc bao nhiêu thì làm ạ, em cảm ơn rất nhiều!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
N
4
3 tháng 10 2023
2
a) Chất rắn màu đen và xanh lơ tan dần, xuất hiện dung dịch mà xanh lam.
\(CuO+H_2SO_4\rightarrow CuSO_4+H_2O\\ Cu\left(OH\right)_2+H_2SO_4\rightarrow CuSO_4+2H_2O\)
b) Chất rắn màu đỏ nâu tan dần, xuất hiện dung dịch màu vàng nâu.
\(Fe_2O_3+6HCl\rightarrow2FeCl_3+3H_2O\\ Fe\left(OH\right)_3+3HCl\rightarrow FeCl_3+3H_2O\)
c) Dần dần xuất hiện kết tủa trắng.
\(H_2SO_4+Ba\left(OH\right)_2\rightarrow BaSO_4+2H_2O\\ H_2SO_4+BaCl_2\rightarrow BaSO_4+2HCl\\ Ba\left(NO_3\right)_2+H_2SO_4\rightarrow BaSO_4+2HNO_3\\ Na_2SO_4+BaCl_2\rightarrow2NaCl+BaSO_4\\ Na_2SO_4+Ba\left(NO_3\right)_2\rightarrow2NaNO_3+BaSO_4\\ Na_2SO_4+Ba\left(OH\right)_2\rightarrow2NaOH+BaSO_4\)
3 tháng 10 2023
\(3:\\ 1/Fe+2HCl\rightarrow FeCl_2+H_2\\ 2/2H_2SO_4+Cu\xrightarrow[t^0]{đặc}CuSO_4+SO_2+2H_2O\\ 3/Fe_2O_3+6HCl\rightarrow2FeCl_3+3H_2O\\ 4/SO_3+H_2O\rightarrow H_2SO_4\\ 5/Ba\left(NO_3\right)_2+H_2SO_4\rightarrow BaSO_4+2HNO_3\\ 6/H_2SO_4+Ba\left(OH\right)_2\rightarrow BaSO_4+2H_2O\)
H9
HT.Phong (9A5)
CTVHS
8 tháng 10 2023
Dạng 3:
Bài 1:
a) Số lượng số hạng là:
\(\left(999-1\right):1+1=999\) (số hạng)
Tổng dãy là:
\(A=\left(999+1\right)\cdot999:2=499500\)
b) Số lượng số hạng là:
\(\left(100-7\right):3+1=32\) (số hạng)
Tổng dãy là:
\(S=\left(100+7\right)\cdot32:2=1712\)
AH
Akai Haruma
Giáo viên
27 tháng 8 2021
Đây là bài bạn phải nộp cho thầy nên mình sẽ không làm chi tiết. Nhưng mình có thể gợi ý cho bạn như sau:
1.
Đối với tỉ lệ thức đã cho, mỗi phân số ta nhân cả tử và mẫu với 4, 3, 2. Khi đó, ta thu được 1 tỉ lệ thức mới
Dùng tỉ lệ thức trên, áp dụng tính chất dãy tỉ số bằng nhau (cộng), ta thu được $12x=8y=6z(*)$
Tiếp tục áp dụng tính chất dãy tỉ số bằng nhau cho $(*)$ dựa theo điều kiện $x+y+z=18$ ta sẽ tính được $x,y,z$ thỏa mãn.
AH
Akai Haruma
Giáo viên
27 tháng 8 2021
2.
Áp dụng tính chất dãy tỉ số bằng nhau (cộng) cho 3 phân số đầu tiên, ta sẽ tìm được tổng $x+y+z$
Khi tìm được tổng $x+y+z$, cộng vào 3 phân số đầu tiên trong bài, mỗi phân số cộng thêm 1. Khi đó, ta thu được tỉ lệ thức $\frac{m}{x}=\frac{n}{y}=\frac{p}{z}(*)$ với $m,n,p$ đã tính được dựa theo giá trị $x+y+z$.
Áp dụng tính chất dãy tỉ số bằng nhau cho tỉ lệ thức $(*)$, kết hợp với kết quả $x+y+z$ thì bài toán đã rất quen thuộc rồi.
20 tháng 8 2021
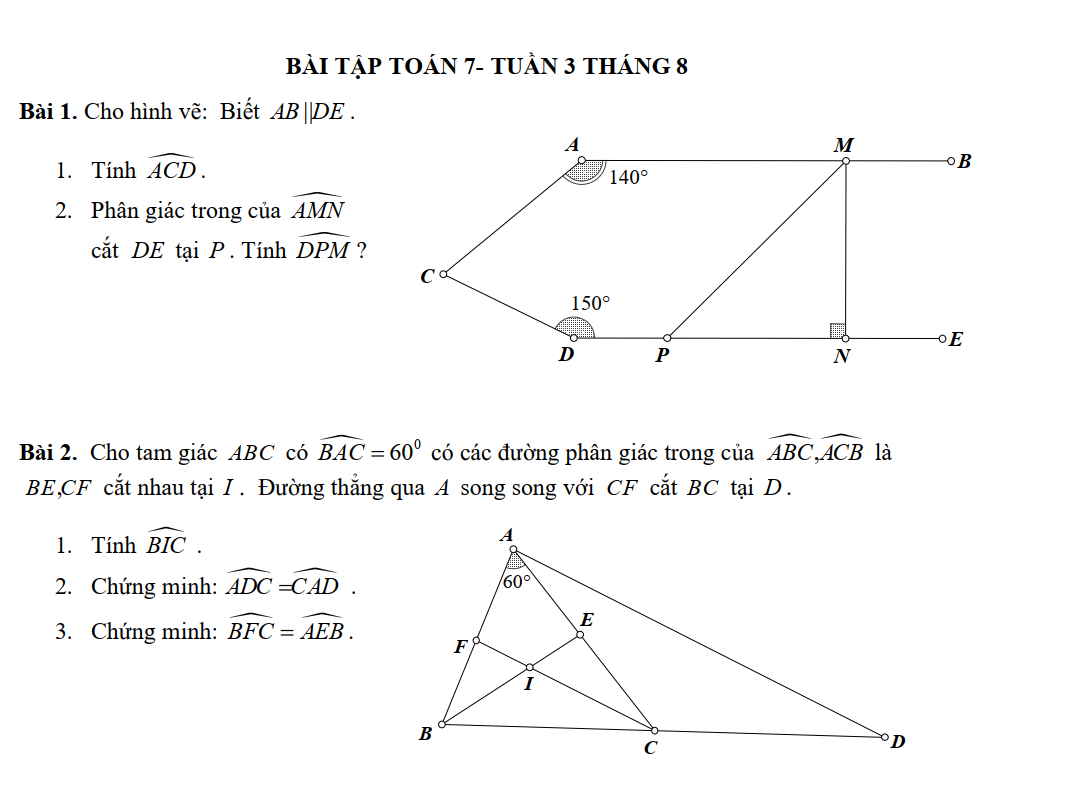
Bài 1:
1) Kẻ tia Cx//AB//DE
Ta có: Cx//AB
\(\Rightarrow\widehat{BAC}+\widehat{ACx}=180^0\)(2 góc trong cùng phía)
\(\Rightarrow\widehat{ACx}=180^0-\widehat{BAC}=180^0-140^0=40^0\)
Ta có: Cx//DE
\(\Rightarrow\widehat{xCD}+\widehat{CDE}=180^0\)( 2 góc trong cùng phía)
\(\Rightarrow\widehat{xCD}=180^0-\widehat{CDE}=180^0-150^0=30^0\)
\(\Rightarrow\widehat{ACD}=\widehat{ACx}+\widehat{xCD}=40^0+30^0=70^0\)
2) Ta có AB//DE(gt)
Mà DE⊥MN
=> AB⊥MN =>\(\widehat{AMN}=90^0\Rightarrow\dfrac{1}{2}\widehat{AMN}=45^0\Rightarrow\widehat{AMP}=45^0\) (do MP là tia phân giác \(\widehat{AMN}\))
Ta có AB//DE
=> \(\widehat{AMP}+\widehat{DPM}=180^0\) (2 góc trong cùng phía)
\(\Rightarrow\widehat{DPM}=180^0-\widehat{AMP}=180^0-45^0=135^0\)
1 tháng 10 2021
tam giác ABM và tam giác KBM có
BK=BA
BM là cạnh chung
BM là phân giác góc B = > góc ABM = góc KBM
=> tam giác ABM = tam giác KBM ( c.g.c)
1 tháng 10 2021
a: Xét ΔABM và ΔKBM có
BA=BK
\(\widehat{ABM}=\widehat{KBM}\)
BM chung
Do đó: ΔABM=ΔKBM
b: Ta có: ΔABM=ΔKBM
nên \(\widehat{BAM}=\widehat{BKM}\)
hay \(\widehat{BKM}=90^0\)
Xét ΔAME vuông tại A và ΔKMC vuông tại K có
MA=MK
\(\widehat{AME}=\widehat{KMC}\)
Do đó: ΔAME=ΔKMC
Suy ra: ME=MC
HN
7 tháng 8 2021
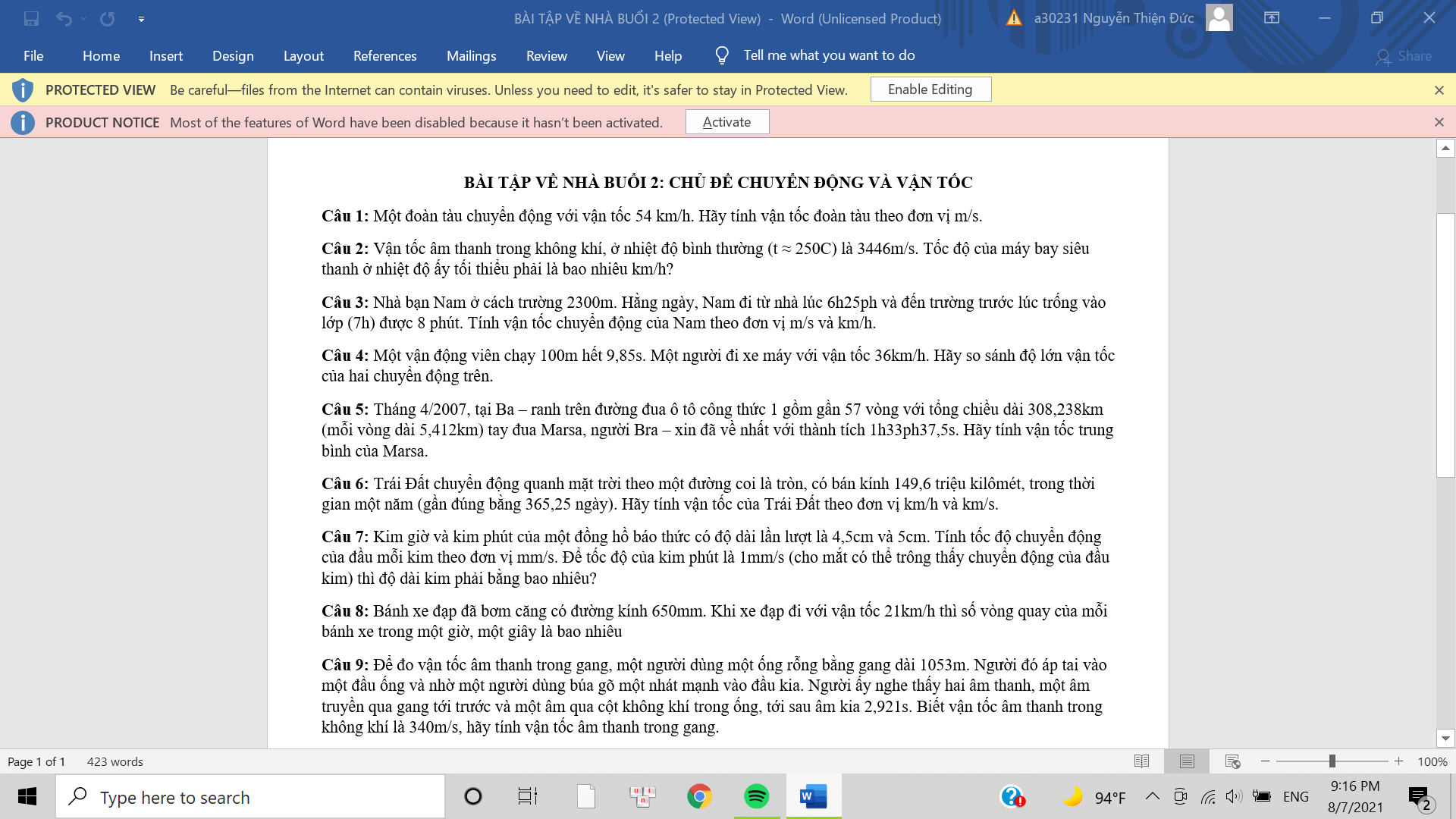
Bài 3 :
Đổi : s= 2300m = 2,3 km
Nam đến trường lúc : 7h - 8 phút = 6h52ph
Tổng thời gian Nam đã đi là :t = 6h52ph - 6h25ph = 27ph = 0.45h
Vận tốc của Nam là : v = \(\dfrac{s}{t}\) = \(\dfrac{2.3}{0.45}\) = \(\dfrac{46}{9}\)( km/h )
đổi ra m/s thì bằng \(\dfrac{46}{9}\) : 3,6 =1.41 m/s
bài 4 :
Vận tốc của vận động viên chạy là : v = \(\dfrac{S}{t}\) = \(\dfrac{100}{9.85}\) = 10,15 (m/s) = 36,54 km/h
so sánh 36 km/h > 36.54 km/h => vận động viên chạy nhanh hơn xe máy
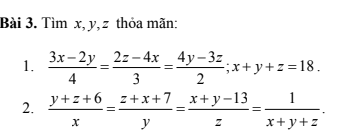
đề bài đâu bạn mình ko thấy
mình cập nhật r nhé