Cho một tam giác vuông, nếu tăng các cạnh góc vuông lên 2cm và 3cm thì diện tích sẽ tăng thêm 50cm2. Nếu giảm cả hai cạnh đi 2cm thì diện tích sẽ giảm đi 32cm2. Tính hai cạnh góc vuông của tam giác.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
14 tháng 8 2019
Gọi x (cm) , y (cm) là độ dài hai cạnh góc vuông của tam giác vuông (x > 2, y > 4).
Diện tích tam giác ban đầu là 1 2 xy (cm2)
+ Tăng mỗi cạnh lên 3cm thì tam giác vuông mới có độ dài 2 cạnh là x + 3(cm) và y + 3 (cm)
Diện tích tam giác mới là: 1 2 ⋅ ( x + 3 ) ( y + 3 ) (cm2)
Diện tích tăng thêm 36cm2 nên ta có phương trình:
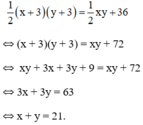
+ Giảm một cạnh 2cm và giảm cạnh kia 4cm thì tam giác vuông mới có 2 cạnh là : x – 2 (cm) và y – 4 (cm).
Diện tích tam giác mới là: 1 2 ( x − 2 ) ( y − 4 ) (cm2).
Diện tích giảm đi 26cm2 nên ta có phương trình
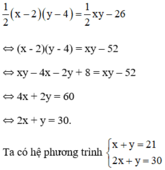
Lấy phương trình thứ hai trừ phương trình thứ nhất ta được:
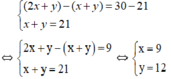
Vậy tam giác có hai cạnh lần lượt là 9cm và 12cm.
Kiến thức áp dụng
Giải bài toán bằng cách lập hệ phương trình :
Bước 1 : Lập hệ phương trình
- Chọn các ẩn số và đặt điều kiện thích hợp
- Biểu diễn các đại lượng chưa biết và đã biết theo ẩn
- Lập các phương trình biểu thị mối quan hệ giữa các đại lượng theo đề bài.
- Từ các phương trình vừa lập rút ra được hệ phương trình.
Bước 2 : Giải hệ phương trình (thường sử dụng phương pháp thế hoặc cộng đại số).
Bước 3 : Đối chiếu nghiệm với điều kiện và kết luận.
3 tháng 3 2021
một vật có khối lượng 124g và thể tích 15 cm3 là hợp kim của đồng và kẽm . tính xem trong đó có bao nhiêu gam đồng và bao nhiêu gam kẽm , biết rằng cứ 89 g đồng thì có thể tích là 10 cm3 và 7g kẽm có thể tích là 1 cm3
7 tháng 3 2021
Gọi cạnh góc vuông lớn và cạnh góc vuông nhỏ lần lượt là a(cm) và b(cm)(Điều kiện: a>0; b>0; a>b)
Diện tích tam giác vuông là:
\(\dfrac{1}{2}ab\left(cm^2\right)\)
Vì khi tăng cạnh lớn lên 5cm và tăng cạnh nhỏ thêm 3cm thì diện tích tăng thêm 80cm2 nên ta có phương trình:
\(\dfrac{1}{2}\left(a+5\right)\left(b+3\right)=\dfrac{1}{2}ab+80\)
\(\Leftrightarrow\dfrac{1}{2}\left(ab+3a+5b+15\right)=\dfrac{1}{2}ab+80\)
\(\Leftrightarrow\dfrac{1}{2}ab+\dfrac{3}{2}a+\dfrac{5}{2}b+\dfrac{15}{2}=\dfrac{1}{2}ab+80\)
\(\Leftrightarrow\dfrac{3}{2}a+\dfrac{5}{2}b=\dfrac{145}{2}\)
\(\Leftrightarrow3a+5b=145\)(1)
Vì khi giảm mỗi cạnh đi 2cm thì diện tích giảm 35cm2 nên ta có phương trình:
\(\dfrac{1}{2}\left(a-2\right)\left(b-2\right)=\dfrac{1}{2}ab-35\)
\(\Leftrightarrow\dfrac{1}{2}\left(ab-2a-2b+4\right)=\dfrac{1}{2}ab-35\)
\(\Leftrightarrow\dfrac{1}{2}ab-a-b+2=\dfrac{1}{2}ab-35\)
\(\Leftrightarrow-a-b=-37\)
hay a+b=37(2)
Từ (1) và (2) ta lập được hệ phương trình:
\(\left\{{}\begin{matrix}3a+5b=145\\a+b=37\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3a+5b=145\\3a+3b=111\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2b=34\\a+b=37\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=17\\a=37-b=37-17=20\end{matrix}\right.\)(thỏa ĐK)
Vậy: Độ dài hai cạnh góc vuông lần lượt là 17cm và 20cm
4 tháng 4 2017
Bài giải:
Gọi x (cm), y (cm) là độ dài hai cạnh góc vuông của tam giác vuông. Điều kiện x > 0, y > 0.
Tăng mỗi cạnh lên 3 cm thì diện tích tăng them 36 cm2 nên ta được:
=
+ 36
Một cạnh giảm 2 cm, cạnh kia giảm 4 cm thì diện tích của tam giác giảm 36 cm2 nên ta được
=
- 26
Ta có hệ phương trình
Giải ra ta được nghiệm x = 9; y = 12.
Vậy độ dài hai cạnh góc vuông là 9 cm, 12 cm.
Lời giải:
Gọi độ dài cạnh góc vuông ban đầu là $a,b$ (cm)
Theo bài ra ta có:
$(a+2)(b+3)=ab+50$
$\Leftrightarrow 3a+2b=44(1)$
Và:
$(a-2)(b-2)=ab-32$
$\Leftrightarrow -2a-2b+4=-32$
$\Leftrightarrow a+b=18(2)$
Từ $(1); (2)\Rightarrow a=8; b=10$ (cm)