Cho hình thang ABCD có đáy AB,CD
A, Nếu AD//BC .CMR AD=BC và AB//BC
B,Nếu AB=CD .CMR AD//BC và AD=CD
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Vì ABCD là hình thang có đáy AB,CD và AB=CD=>ABCD là hình thang=>BC=AD,BC//AD.
chúc bạn học tốt nhớ k cho mình nha!
A B C D
Hình thang ABCD có AB=CD và AB//CD nên hình thang ABCD là hình bình hành.
=> \(BC=AD,BC//AD\)


Bài 1: △ABD=△BAC(c−g−c)△ABD=△BAC(c−g−c)
=>AC=BD=>AC=BD
△ACD=△BDC(c−c−c)△ACD=△BDC(c−c−c)
=>ADCˆ=BCDˆ=>ADC^=BCD^
Mà ADCˆ+DABˆ+ABCˆ+BCDˆ=360oADC^+DAB^+ABC^+BCD^=360o
=>2(DABˆ+ADCˆ)=360o=>2(DAB^+ADC^)=360o
=>DABˆ+ADCˆ=180o=>DAB^+ADC^=180o
=>AB//CD=>AB//CD
=>ABCD=>ABCD là hình thang mà có 2 góc ở đáy bằng nhau nên lf thang cân ![]()
Bài 4: chắc mấy bạn ở dưới vẽ sai hình :3 -_-
hình vẽ chính xác là ta vẽ được một hình thang cân với AD//BCAD//BC sẽ có được đầy đủ điều kiện đề bài đưa ra ![]()
Giải:
△ADB=△DAC△ADB=△DAC (c-c-c)
=>DABˆ=ADCˆ=>DAB^=ADC^
Từ đây chứng minh như câu 1 là =>đpcm ![]() )
)

a: Gọi K là giao của AD và BC
Xét ΔKDC có AB//DC
nên KA/AD=KB/BC
=>KA/KB=AD/BC
Xét ΔKMN có AB//MN
nên KA/AM=KB/BN
=>KA/KB=AM/BN
=>AM/BN=AD/BC
=>AM/AD=BN/BC
b: AM/AD=BN/BC
=>AD/AM=BC/BN
=>AD/AM-1=BC/BN-1
=>\(\dfrac{AD-AM}{AM}=\dfrac{BC-BN}{BN}\)
=>DM/AM=NC/BN
=>MA/MD=BN/NC
c: AM/AD=BN/BC
=>AM/AD-1=BN/BC-1
=>(AM-AD)/AD=(BN-BC)/BC
=>-MD/AD=-CN/BC
=>MD/AD=CN/BC

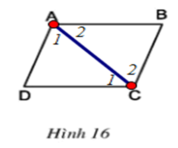
Hình thang ABCD có đáy AB, CD ⇒ AB // CD ⇒ ∠A2 = ∠C1 ̂ (hai góc so le trong)
Lại có: AD // BC ⇒ ∠A1 = ∠C2 (hai góc so le trong)
Xét ΔABC và ΔCDA có:
∠A2 = ∠C1 (cmt)
AC chung
∠A1 = ∠C2 (cmt)
⇒ ΔABC = ΔCDA (g.c.g)
⇒ AD = BC, AB = CD (các cặp cạnh tương ứng)
b)
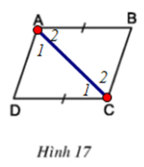
Xét ΔABC và ΔCDA có:
AC chung
∠A2 = ∠C1 (cmt)
AB = CD
⇒ ΔABC = ΔCDA (c.g.c)
⇒ AD = BC (hai cạnh tương ứng)
∠A1 = ∠C2 (hai góc tương ứng) ⇒ AD // BC (hai góc so le trong bằng nhau)