Một gia đình cần ít nhất 900g chất protein và 400g lipit trong thức ăn mỗi ngày. Biết rằng thịt bò chứ 80% protein và 20% lipit. Thịt lợn chứa 60% protein và 40% lipit. Biết rằng gia đình này chỉ mua nhiều nhất là 1600g thịt bò và 1100g thịt lợn, giá tiền 1kg thịt bò là 45000 đồng, 1kg thịt lợn là 35 nghìn đồng. Gia đình đó phải mua bao nhiêu kg thịt mỗi loại để chi phí là ít nhất
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án A
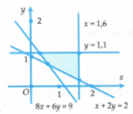
Gọi a, b lần lượt là số kg thịt bò và thịt lợn mà gia đình đó cần mua đảm bảo lượng protein và lipit trong thức ăn. Theo bài ra ta có số tiền gia đình cần trả là 160a + 110b với a, b thỏa mãn



Do đó, tổng số tiền họ phải trả là ít nhất mà vẫn đảm bảo lượng protein và lipit trong thức ăn thì x = a = 0,3; y = b = 1,1
![]()

Tham khảo:
a) Giả sử gia đình đó mua x kilôgam thịt bò và y kilôgam thịt lợn.
Số lượng thịt bò và thịt lợn phải là một số không âm nên ta có: \(x \ge 0,y \ge 0\).
Một gia đình cần ít nhất 900 đơn vị protein trong thức ăn mỗi ngày nên ta có: \(800x + 600y \ge 900 \Leftrightarrow 8x + 6y \ge 9\)
Một gia đình cần ít nhất 400 đơn vị protein trong thức ăn mỗi ngày nên ta có: \(200x + 400y \ge 400 \Leftrightarrow x + 2y \ge 2\)
Vì gia đình này chỉ mua nhiều nhất là 1,6 kg thịt bò và 1,1 kg thịt lợn nên ta có:
\(x \le 1,6\) và \(y \le 1,1\).
Vậy ta có hệ: \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\8x + 6y \ge 9\\x + 2y \ge 2\\x \le 1,6\\y \le 1,1\end{array} \right.\)
Miền nghiệm của hệ là tứ giác ABCD với
A(1,6;0,2) (giao của d’ và đường thẳng x=1,6)
B(1,6;1,1) (giao của đường thẳng x=1,6 và đường thẳng y=1,1)
C(0,3;1,1) (giao của d và đường thẳng y=1,1)
D(0,6;0,7) (giao của d và d’)
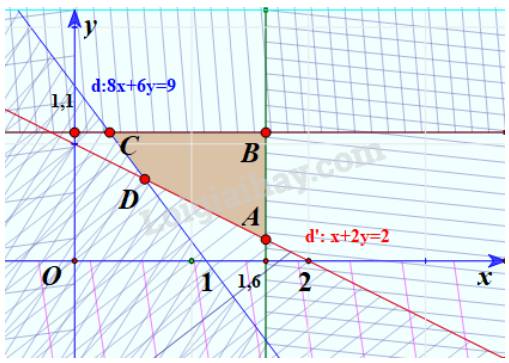
b) Vì số tiền mỗi kg thịt bò và thịt lợn lần lượt là 250 nghìn đồng và 160 nghìn đồng nên ta có
\(F\left( {x;y} \right) = 250x + 160y\)(nghìn đồng)
c)
Ta cần tìm giá trị lớn nhất của F(x;y) khi (x;y) thỏa mãn hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\8x + 6y \ge 9\\x + 2y \ge 2\\x \le 1,6\\y \le 1,1\end{array} \right.\)
Ta có F(1,6;0,2)=250.1,6+160.0,2=432.
F(1,6;1,1)=250.1,6+160.1,1=576
F(0,3;1,1)=251
F(0,6;0,7)=262
Giá trị nhỏ nhất là F(0,3;1,1)=251.
Vậy để chi phí ít nhất thì cần mua 0,3kg thịt bò và 1,1 thịt lợn.
Chú ý
Đơn vị của F phải là nghìn đồng.

a) Mỗi gam thịt bò chứa 0,261 g protein.
Người đó ăn x gam thịt bò, tương ứng 0,261.x g protein
Mỗi quả trứng nặng 44 g chứa 5,7 g protein.
Người đó ăn y quả trứng, tương ứng 5,7.x g protein
Như vậy lượng protein trong khẩu phần ăn hằng ngày của người đó là: \(0,261x + 5,7y\)
Mỗi ngày, người đó cần không quá 60 g protein nên ta có bất phương trình: \(0,261x + 5,7y \le 60\)
b)
- Nếu người đó ăn 150 g thịt bò và 2 quả trứng (mỗi quả 44 g) trong một ngày thì lượng protein tương ứng: \(150.0,261 + 2.5,7 = 50,55 \le 60\) \( \Rightarrow \)Kết luận: phù hợp.
- Nếu người đó ăn 200 g thịt bò và 2 quả trứng (mỗi quả 44 g) trong một ngày thì lượng protein tương ứng: \(200.0,261 + 2.5,7 = 63,6 > 60\) \( \Rightarrow \)Kết luận: Không phù hợp.

Tính tổng số gam prôtêin, lipit, gluxit cung cấp cho cơ thể trong một ngày.
1. Tính được số năng lượng của mỗi chất
Số năng lượng prôtêin chiếm 19% là:2200.19/100 = 418 Kcal
Số năng lượng lipit chiếm 13% là:2200.13/100 = 286 Kcal
Số năng lượng gluxit chiếm (100% - (19% + 13%) = 68%) là:2200.68/100 = 1496 Kcal
2. Tính được số gam prôtêin, lipit, gluxit
Lượng prôtêin là: 418/4,1 = 102 (gam)Lượng lipit là: 286/9,3 = 30,8 (gam)Lượng gluxit là: 1496/4,3 = 347,9 (gam)