giải bài toán bằng cách lập phương trình
Một canô xuôi dòng từ bến A đến bến B mất 4 giờ và ngược dòng từ bến B về bến A mất 5 giờ. Tính khoảng cách giữa bến A đến bến B, biết rằng vận tốc của dòng nước là 2km/h
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x (km) là khoảng cách giữa hai bến A và B, với x > 0.

Vì vận tốc xuôi dòng lớn hơn vận tốc ngược dòng chính bằng 2 lần vận tốc dòng nước nên ta có phương trình:
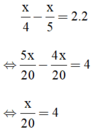
x = 80 (thỏa mãn điều kiện).
Vậy khoảng cách giữa hai bến A và B là 80km.
(Giải thích tại sao hiệu vận tốc xuôi dòng và ngược dòng bằng 2 lần vận tốc dòng nước:
Nếu gọi vận tốc canô là v (km/h), vận tốc dòng nước là a (km/h), ta có:
Khi xuôi dòng: vận tốc canô = v + a
Khi ngược dòng: vận tốc canô = v - a
Hiệu vận tốc = v + a - (v - a) = 2a = 2 vận tốc dòng nước.)

gọi vận tốc thực là x (x>2)
=> vxuôi là x+2 (km)
vngược là x-2(km)
ta có pt
5(x+2)=6(x-2)
=> x = 22 (thỏa mãn bài)
=> AB= 22km

LƯU Ý
Các bạn học sinh KHÔNG ĐƯỢC đăng các câu hỏi không liên quan đến Toán, hoặc các bài toán linh tinh gây nhiễu diễn đàn. Online Math có thể áp dụng các biện pháp như trừ điểm, thậm chí khóa vĩnh viễn tài khoản của bạn nếu vi phạm nội quy nhiều lần.
Chuyên mục Giúp tôi giải toán dành cho những bạn gặp bài toán khó hoặc có bài toán hay muốn chia sẻ. Bởi vậy các bạn học sinh chú ý không nên gửi bài linh tinh, không được có các hành vi nhằm gian lận điểm hỏi đáp như tạo câu hỏi và tự trả lời rồi chọn đúng.
Mỗi thành viên được gửi tối đa 5 câu hỏi trong 1 ngày
Các câu hỏi không liên quan đến toán lớp 1 - 9 các bạn có thể gửi lên trang web h.vn để được giải đáp tốt hơn.

Gọi khoảng cách giữa hai bến A và B là x (km), điều kiện:
x > 0
Vận tốc canô đi từ A đến B là x/3 (km/h)
Vận tốc canô đi từ B về A là x/4 (km/h)
Do vận tốc của dòng nước là 2,5 km/h, vận tốc thực canô không đổi nên ta có PT
\(\frac{x}{3}-2,5=\frac{x}{4}+2,5\)
⇔ 4x – 30 = 3x + 30
⇔ x = 60 (Thỏa mãn điều kiện)
Vậy khoảng cách giữa hai bến A và B là 60 km.

Gọi vận tốc thật của cano là x
Theo đề, ta có: 2(x+3)=3(x-3)
=>2x+6=3x-9
=>-x=-15
=>x=15
=>AB=2*(15+3)=36km

Gọi khoảng cách từ A đến B là x ( km ) ( x>0 )
Vận tốc xuôi dòng là: \(\dfrac{x}{4}\) (h)
Vận tốc ngược dòng là: \(\dfrac{x}{5}\) (h)
Theo đề bài ta có pt:
\(\dfrac{x}{4}-\dfrac{x}{5}=2.2\)
\(\Leftrightarrow\dfrac{5x-4x}{20}=\dfrac{80}{20}\)
\(\Leftrightarrow x=80\left(tm\right)\)
Vậy khoảng cách từ A đến B là 80km
Gọi vận tốc cano khi nước lặng là x km/h với x>2
Vận tốc cano khi xuôi dòng: x+2 (km/h)
Quãng đường cano đi xuôi dòng: \(4\left(x+2\right)\)
Vận tốc cano khi ngược dòng: \(x-2\) (km/h)
Quãng đường cano đi ngược dòng: \(5\left(x-2\right)\) (km/h)
Do độ dài quãng đường xuôi dòng và ngược dòng như nhau nên ta có pt:
\(4\left(x+2\right)=5\left(x-2\right)\)
\(\Leftrightarrow x=18\) (km/h)
Độ dài AB: \(4\left(18+2\right)=80\left(km\right)\)

Gọi quãng đường AB là l
vận tốc của ca nô là : \(V_c\)
vận tốc của dòng nước là: \(V_n\)
*) Khi ca nô đi xuôi dòng từ A-> B thì \(l=4\left(V_c+V_n\right)\)
*) Khi ca nô đi ngược dòng từ A -> B thì \(l=5\left(V_c-V_n\right)\)
=> \(4\left(V_c+V_n\right)=5\left(V_c-V_n\right)=>4V_c+4V_n=5V_c-5V_n=>9V_n=V_c=>V_c=180km\)/h
=>l=5.160=800km.
Gọi X là vận tốc thức của cano
Khi xuôi dòng ta có: AB= (x+2)4
Khi ngược dòng ta có: AB = (x-2),5
Từ đây ta có pt (x+2)4= (x-2).5
Tìm đc x= 18 vậy S AB= (18+2).4=80 km
Gọi vận tốc thực của ca nô là x km/h thì vận tốc xuôi dòng và ngược dòng của ca nô lần lượt là x + 2 km/h và x - 2 km/h nên khoảng cách từ bến A đến bến B là : 4(x + 2) = 5(x - 2) <=> 4x + 8 = 5x - 10 => 5x = 4x + 8 + 10 = 4x + 18 => 18 = 5x - 4x = x
=> 4(x + 2) = 4.(18 + 2) = 4.20 = 80 hay 5(x - 2) = 5.(18 - 2) = 5.16 = 80. Vậy khoảng cách từ bến A đến bến B là 80 km.