Câu này mình nghĩ ra.
Cho \(\Delta ABC\), các đường phân giác trong AD, BE, CF đồng quy tại I\(\left(D\in BC;E\in AC;F\in AB\right)\). Chứng minh rằng \(\frac{ID}{IA}+\frac{IE}{IB}+\frac{IF}{IC}\ge\frac{3}{2}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

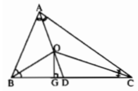
Để chứng minh ∠(BOG) = ∠(COD), ta chứng minh ∠(BOD) = ∠(GOC).
+) Tổng ba góc trong 1 tam giác bằng 180º nên :
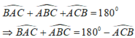
+) Xét tam giác OAB, ta có góc ∠BOD là góc ngoài tam giác tại đỉnh O nên:
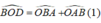
Lại có: BO và AO là tia phân giác của góc B và góc A nên:
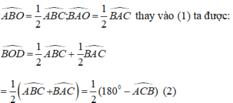
Xét tam giác vuông OCG ta có:
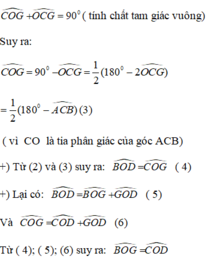

a, Xét tg BAE và tg BDE ( \(\widehat{BAE}=\widehat{BDE}=90^0\))
BA=BD (gt)
BE chung
=> tg BAE = tg BDE ( ch-cgv)
=> AE=ED
Ta có \(\hept{\begin{cases}BA=BD\left(gt\right)\\AE=ED\left(cmt\right)\end{cases}}< =>\)BE trung trực AD (đpcm)
b, +ED vuông BC
+ AH vuông BC
=> AH//DE
=> \(\widehat{HAD}=\widehat{ADE}\)( So le trong) (2)
Lại có gọi m là giao 2 đường thẳng BE và AD
vì BE trung trực AD =>+ \(\widehat{AME}=\widehat{EMD}=90^{0^{ }}\)
Xét tg AEM và tg DEM có \(\left(\widehat{AME}=\widehat{EMD}=90^0\left(cmt\right)\right)\)
+ AD = ED (cma)
+ EM chung
=> tg AEM = tg DEM ( ch-cgv)
=> \(\widehat{DAE}=\widehat{ADE}\)(2)
tỪ (1) VÀ (2) => \(\widehat{HAD}=\widehat{DAE}\)=> AD phân giác góc AHC
Đặt \(BC=a;AC=b;AB=c\left(a,b,c>0\right)\)
\(\Delta BCF\)có phân giác trong BI \(\left(I\in CF\right)\)\(\Rightarrow\frac{IF}{IC}=\frac{BF}{BC}\)(1)
\(\Delta ABC\)có phân giác trong CF \(\left(F\in AB\right)\)\(\Rightarrow\frac{BF}{BC}=\frac{AF}{AC}=\frac{BF+AF}{BC+AC}=\frac{AB}{BC+AC}=\frac{c}{a+b}\)(2)
Từ (1) và (2) \(\Rightarrow\frac{IF}{IC}=\frac{c}{a+b}\)
Tương tự, ta có \(\frac{IE}{IB}=\frac{b}{c+a}\); \(\frac{ID}{IA}=\frac{a}{b+c}\)
Từ đó \(\frac{ID}{IA}+\frac{IE}{IB}+\frac{IF}{IC}=\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}\)
Ta cần chứng minh \(\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}\ge\frac{3}{2}\)với \(a,b,c>0\)
Thật vậy: Ta chứng minh bất đẳng thức phụ \(\left(x+y+z\right)\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)\ge9\)với \(x,y,z>0\)
Áp dụng bất đẳng thức Cô-si cho 3 số dương \(x,y,z\), ta có: \(x+y+z\ge3\sqrt[3]{xyz}\)
Tương tự, ta có \(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\ge3\sqrt[3]{\frac{1}{xyz}}\)
Từ đó \(\left(x+y+z\right)\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)\ge3\sqrt[3]{xyz}.3\sqrt[3]{\frac{1}{xyz}}=9\)
Vậy bất đẳng thức được chứng minh.
Áp dụng bất đẳng thức trên, ta có: \(\left[\left(a+b\right)+\left(b+c\right)+\left(c+a\right)\right]\left(\frac{1}{a+b}+\frac{1}{c+a}+\frac{1}{a+b}\right)\ge9\)
\(\Leftrightarrow2\left(a+b+c\right)\left(\frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{c+a}\right)\ge9\)
\(\Leftrightarrow\left(a+b+c\right)\left(\frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{c+a}\right)\ge\frac{9}{2}\)
\(\Leftrightarrow\frac{a+b+c}{a+b}+\frac{a+b+c}{b+c}+\frac{a+b+c}{c+a}\ge\frac{9}{2}\)
\(\Leftrightarrow1+\frac{c}{a+b}+1+\frac{b}{c+a}+1+\frac{a}{b+c}\ge\frac{9}{2}\)
\(\Leftrightarrow\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}\ge\frac{3}{2}\)
\(\Rightarrow\)đpcm