Hàm số \(y=\sqrt{2018x-x^2}\) nghịch biến trên khoảng nào dưới đây
A:(1010;2018)
B:(2018;\(+\infty\))
C:(0;1009)
D:(1;2018)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan

CM
5 tháng 7 2018
Đáp án B
Quan sát bảng biến thiên ta thấy trong khoảng (-1;2) hàm số có f'(x)<0 nên nghịch biến trong khoảng (-1;2)

NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 3 2021
\(y'=x^2-2x+1=\left(x-1\right)^2\ge0\) ;\(\forall x\in R\)
\(\Rightarrow\) Hàm đồng biến trên R

CM
24 tháng 9 2017
Đáp án C
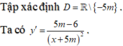
Để hàm số nghịch biến trên khoảng ( 10 ; + ∞ ) thì
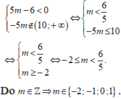

CM
11 tháng 10 2018
Đáp án C
f ' x > 0 ⇔ 1 < x < 2 ⇒ hàm số đồng biến trên khoảng (1;2)




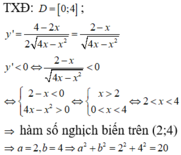

ĐKXĐ: \(x\in\left[0;2018\right]\)
\(y'=\dfrac{1009-x}{\sqrt{2018x-x^2}}=0\Rightarrow x=1009\)
Hàm đồng biến trên \(\left(0;1009\right)\)