Hai viên bi nhỏ có khối lượng m1 = 400g, m2 = 500g. Viên bi thứ nhất đang đứng yên v1 = 0, viên bi thứ hai chuyển động với vận tốc v2 = 2m/s và va chạm xuyên tâm với viên bi thứ nhất. Sau va chạm, viê...

CV

Công Việc

12 tháng 2 2022

Hai viên bi nhỏ có khối lượng m1 = 400g, m2 = 500g. Viên bi thứ nhất đang đứng yên v1 = 0, viên bi thứ hai chuyển động với vận tốc v2 = 2m/s và va chạm xuyên tâm với viên bi thứ nhất. Sau va chạm, viên bi thứ nhất chuyển động với vận tốc 1,5 m/s. Tìm độ lớn và chiều của viên bi 2 sau va chạm? Bỏ qua mọi lực cản. ___Giúp mình với, mình đang cần gấp lắm mọi người ơiiiiiii...

Đọc tiếp

#Vật lý lớp 10

0

HD

Hoàng Đức Long

24 tháng 6 2019

Một viên bi thứ nhất có khối lượng m 1 = 200 g chuyển động với vận tốc v 1 = 4 m / s đến va chạm với viên bi thứ hai có khối lượng m 2 đang đứng yên. Coi va chạm giữa hai viên bi là hoàn toàn mềm. Cả hai viên bi đều ở trên mặt sàn nằm ngang, không ma sát. Vận tốc của cả hai viên bi sau va chạm bằng 2 m/s....

Đọc tiếp

#Vật lý lớp 10

1

VT

Vũ Thành Nam

24 tháng 6 2019

Lời giải

Sau va chạm 2 viên bị dính vào nhau và cùng chuyển động với cùng một vận tốc => 2 vật va chạm mềm.

Chọn chiều dương là chiều chuyển động của hai viên bi

Gọi v 1 , v 2 , V lần lượt là vận tốc của viên bi thứ nhất, viên bi thứ hai và của 2 viên bi sau va chạm. Ta có:

m 1 v 1 + m 2 v 2 = m 1 + m 2 V ⇒ V = m 1 v 1 + m 2 v 2 m 1 + m 2 ⇔ 2 = 0 , 2.4 + m 2 .0 0 , 2 + m 2 ⇔ m 2 = 0 , 2 k g = 200 g

Đáp án: B

Đúng(0)

C

Chuyengia247

22 tháng 1 2022

Một viên bi có khối lượng m1=2kg đang chuyển động với vận tốc v1=5m/s đến va chạm vào viên bi thứ hai có khối lượng m2=1kg đang đưng yên. Sau va chạm 2 viên bi chuyển động theo hướng vuông góc với nhau với vận tốc viên bi thứ hai gấp 2 lần viên bi thứ nhất. Tính vận tốc mỗi viên bi sau khi va chạm?

#Vật lý lớp 10

0

VT

Vy Trần

15 tháng 3 2022

Một viên bi thứ nhất có khối lượng m1 = 200 g chuyển động với vận tốc v1 = 4 m/s đến va chạm với viên bi thứ hai có khối lượng m2 đang đứng yên. Coi va chạm giữa hai viên bi là hoàn toàn mềm. Cả hai viên bi đều ở trên mặt sàn nằm ngang, không ma sát. Vận tốc của cả hai viên bi sau va chạm bằng 2 m/s. Khối lượng của viên bi thứ hai...

Đọc tiếp

#Vật lý lớp 10

1

NT

nguyễn thị hương giang

15 tháng 3 2022

Viên bi thứ hai đứng yên\(\Rightarrow v_2=0\)m/s

Bảo toàn động lượng: \(\overrightarrow{p_1}+\overrightarrow{p_2}=\overrightarrow{p}\)

\(\Rightarrow m_1v_1+m_2v_2=\left(m_1+m_2\right)\cdot V\)

\(\Rightarrow0,2\cdot4=\left(0,2+m_2\right)\cdot2\)

\(\Rightarrow m_2=0,2kg=200g\)

Đúng(2)

HD

Hoàng Đức Long

5 tháng 11 2019

Một viên bi khối lượng m 1 = 500g đang chuyển động với vận tốc v 1 = 4m/s đến chạm vào bi thứ hai đang nằm yên có khối lượng m 2 = 300g. Sau va chạm chúng dính lại chuyển động cùng vận tốc (Bỏ qua ma sát).Vận tốc của hai bi sau va chạm là A. 2 m/s. B. 2,5 m/s. C. 3,5 m/s....

Đọc tiếp

#Mẫu giáo

1

VT

Vũ Thành Nam

5 tháng 11 2019

Đáp án B

Áp dụng định luật bảo toàn động lượng đối với hệ vật trước và sau khi va chạm ta có:

Đúng(0)

HD

Hoàng Đức Long

31 tháng 7 2019

Cho viên bi một có khối lượng 200g đang chuyển động trên mặt phẳng nằm ngang với vận tốc 5m/s tới va chạm vào viên bi thứ hai có khối lượng 400g đang đứng yên, biết rằng sau va chạm viên bi thứ hai chuyển động với vận tốc 3m/s, chuyển động của hai bi trên cùng một đường thẳng. Xác định độ lớn vận tốc và chiều chuyển động của viên bi một sau va chạm. ...

Đọc tiếp

#Vật lý lớp 10

1

VT

Vũ Thành Nam

31 tháng 7 2019

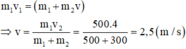
Chọn chiều dương là chiều chuyển động của viên bi một trước lúc va chạm

Theo định luật bảo toàn động lượng

m 1 . v → 1 + m 2 . v → 2 = m 1 . v → 1 ' + m 2 . v → 2 '

Chiếu lên chiều dương ta có

m 1 . v 1 + m 2 .0 = m 1 . v 1 ' + m 2 . v 2 '

⇒ v 1 / = m 1 v 1 − m 2 v 2 m 1 = 0 , 2.5 − 0 , 4.3 0 , 2 = − 1 ( m / s )

Vậy viên bi một sau va chạm chuyển động với vận tốc là 3 m/s và chuyển động ngược chiều với chiều chuyện động ban đầu

Đúng(0)

HD

Hoàng Đức Long

22 tháng 5 2018

Cho viên bi một có khối lượng 200g đang chuyển động trên mặt phẳng nằm ngang vói vận tốc 5m/s tói va chạm vào viên bi thứ hai có khối lượng 400g đang đứng yên, biết rằng sau va chạm viên bi thứ hai chuyển động với vận tốc 3m/s, chuyển động của hai bi trên cùng một đường thẳng. Xác định độ lớn vận tốc và chiều chuyển động của viên bi một sau va chạm. A. 4m /s B. 1...

Đọc tiếp

#Vật lý lớp 10

1

VT

Vũ Thành Nam

22 tháng 5 2018

Chọn chiều dương là chiều chuyển động của viên bi một trước lúc va chạm

Theo định luật bảo toàn động lượng:

m 1 . v → 1 + m 2 v 2 → = m 1 . v → 1 / + m 2 v → 2 /

Chiếu lên chiều dương ta có:

m 1 v 1 + m 2 0 = m 1 v 1 / + m 2 v 2 /

⇒ v 1 / = m 1 v 1 − m 2 v 2 m 1 = 0 , 2.5 − 0 , 4.3 0 , 2 = − 1 m / s

Vậy viên bi một sau va chạm chuyển động với vận tốc là 3 m/s và chuyển động ngược chiều với chiều chuyển động ban đầu.

Chọn đáp án A

Đúng(0)

NV

Nguyễn Vũ Ngọc Anh

6 tháng 2 2021

Một viên bi có khối lượng 500g đang chuyển động không ma sát với vận tốc 4m/s trên mặt phẳng nằm ngang thì va chạm vào viên bi thứ hai có khối lượng 300g đang đứng yên. Sau va chạm, hai viên bi dính làm một. Tìm vận tốc của hai viên bi sau va chạm.

#Vật lý lớp 10

4

NN

Nguyễn Ngọc Lộc

6 tháng 2 2021

Ta thấy : \(\left\{{}\begin{matrix}\Sigma\overrightarrow{P_t}=m_1.\overrightarrow{v_1}+m_2\overrightarrow{v_2}=0,5\overrightarrow{v_1}+0,3\overrightarrow{v_2}\\\Sigma\overrightarrow{P_s}=\left(m_1+m_2\right)\overrightarrow{v}=0,8\overrightarrow{v}\end{matrix}\right.\)

- Áp dụng định luật bảo toàn động lượng ta được :

\(0,8\overrightarrow{v}=0,5\overrightarrow{v_1}+0,3\overrightarrow{v_2}\)

Mà \(v,v_1,v_2\) cùng hướng .

\(\Rightarrow0,5v_1+0,3v_2=0,8v\)

\(\Rightarrow v=\dfrac{0,5v_1+0,3v_2}{0,8}=\dfrac{0,5.4+0,3.0}{0,8}=2,5\left(m/s\right)\)

Vậy ...

Đúng(1)

B

Buddy

6 tháng 2 2021

p=p′m1v1=(m1+m2)vv=m1.v1\m1+m1=0,5.4\0,5+0,3=2,5m/s