Có hai vật m1=2kg, m2=3kg. Chuyển động không ma sát trên một đường thẳng nằm ngang ngược chiều nhau với các tốc độ v1=3m/s, v2=5m/s. Sau va chạm hai vật dính lại cùng vận tốc v. Tìm hướng và độ lớn của vectơ v.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 2 2022
Chọn chiều dương là chiều của vật 1 chuyển động.
Áp dụng định luật bảo toàn động lượng :
\(\left(m_1+m_2\right)v=m_1.v_1-m_2.v_2\)
\(\Leftrightarrow v=\dfrac{m_1.v_1-m_2.v_2}{m_1+m_2}=-1,8\left(m\backslash s\right)\)
\(\Leftrightarrow\) Sau va chạm 2 vật chuyển động cùng chiều vật 2 ban đầu
17 tháng 4 2022
Động lượng vật thứ nhất:
\(p_1=m_1v_1=4m\) (g.m/s)
Động lượng vật thứ hai:
\(p_2=m_2v_2=3m\cdot3=9m\) (g.m/s)
Hai vật va chạm ngược chiều nhau. Bảo toàn động lượng:
\(\overrightarrow{p}=\overrightarrow{p_1}+\overrightarrow{p_2}\Rightarrow p=\left|p_1-p_2\right|=\left|4m-9m\right|=5m\)
Vận tốc của hai vật sau khi chuyển động là:
\(v=\dfrac{p}{m}=\dfrac{5m}{m_1+m_2}=\dfrac{5}{m+3m}=1,25\)m/s
HT
19 tháng 5 2020
Đề bài nhìn dài làm đúng 2 dòng :))
Va chạm đàn hồi nên ta có :\(m_1\overrightarrow{v_1}+m_2\overrightarrow{v_2}=m_1\overrightarrow{v_1'}+m_2\overrightarrow{v_2'}\)
\(\Leftrightarrow m_1v_1+m_2v_2=-m_1v_1'+m_2v_2'\)
\(\Leftrightarrow2.4+4.2=-2.1+4.v_2\Leftrightarrow v_2=4,5\left(m/s\right)\)
AM
7 tháng 2 2022
Xét hệ kín, bảo toàn động lượng ta có: \(m_1v_1-m_2v_2=\left(m_1+m_2\right)v\)
\(\Leftrightarrow0,5.4-0,3.2=\left(0,5+0,3\right)v\)
\(\Leftrightarrow v=1,75\) m/s
Sau va chạm cả hai chuyển động cùng chiều với vật thứ nhất
7 tháng 2 2022
Động lượng vật 1:
\(p_1=m_1\cdot v_1=0,5\cdot4=2kg.m\)/s
Động lượng vật 2:
\(p_2=m_2\cdot v_2=0,5\cdot2=1kg.m\)/s
Hai vật cđ ngược chiều bảo toàn động lượng:
\(m_1\cdot v_1-m_2\cdot v_2=\left(m_1+m_2\right)\cdot v\)
\(\Rightarrow2-1=\left(0,5+0,5\right)\cdot v\)
\(\Rightarrow v=1\)m/s
VT
15 tháng 12 2017
Theo tính chất của và chạm thì: v → 1 ≠ v → 1 / , v → 2 ≠ v → 2 /
Theo phương ngang động lượng của hệ được bảo toàn nên ta có:
m 1 v 1 / + m 2 v 2 / = m 1 v 1 + m 2 v 2 (1)
Động năng của hệ được bảo toàn:
m 1 v 1 / 2 2 + m 2 v 2 / 2 2 = m 1 v 1 2 2 + m 2 v 2 2 2 (2)
Từ (1) ⇒ m 1 ( v 1 − v 1 / ) = m 2 ( v 2 / − v 2 ) (3)
Từ (2) ⇒ m 1 ( v 1 2 − v 1 / 2 ) = m 2 ( v 2 / 2 − v 2 2 ) (4)
Chia (4) cho (3) vế theo vế ta được: v 1 + v 1 / = v 2 / + v 2 (5)
Từ (5) ⇒ v 2 / = v 1 + v 1 / − v 2 (6)
Thay (6) vào (3) ta được:
v 1 / = ( m 1 − m 2 ) v 1 + 2 m 2 v 2 m 1 + m 2 ; v 2 / = ( m 2 − m 1 ) v 2 + 2 m 1 v 1 m 1 + m 2
13 tháng 4 2019
giả sử sau va chạm hệ chuyển động cùng chiều với chuyển động ban đầu của m2
chọn chiều dương cùng chiều chuyển động ban đầu của vật m2
bảo toàn động lượng: \(m_1.\overrightarrow{v_1}+m_2.\overrightarrow{v_2}=\left(m_1+m_2\right).\overrightarrow{V}\)
chiếu lên chiều dương
\(\Rightarrow V=\)\(\frac{1}{3}\)m/s
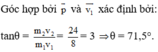
Bảo toàn động lượng:
\(\overrightarrow{p_1}+\overrightarrow{p_2}=\overrightarrow{p}\)
Hai vật chuyển động ngược chiều nhau:
\(\Rightarrow-m_1v_1+m_2v_2=\left(m_1+m_2\right)\cdot v\)
\(\Rightarrow v=\dfrac{-2\cdot3+3\cdot5}{2+3}=1,8\)m/s