Trong các phân số dưới đây, phân số nào bằng\(\frac{6}{5}\) ? Vì sao ?
\(\frac{16}{20}\),\(\frac{12}{10}\),\(\frac{24}{30}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có\(\frac{7}{42}=\frac{1}{6}\)
\(\frac{12}{18}=\frac{3x4}{6x3}=\frac{4}{6}=\frac{2}{3}\)
\(\frac{3}{18}=\frac{1}{6}\)
\(\frac{5}{30}=\frac{1}{6}\)
\(\frac{16}{24}=\frac{8x2}{8x3}=\frac{2}{3}\)
Ta có \(\frac{7}{42}=\frac{3}{18}=\frac{5}{30}=\frac{1}{6}\)
\(\frac{12}{18}=\frac{16}{24}=\frac{2}{3}\)
Vậy \(\frac{7}{20}\)và \(\frac{3}{5}\)là các phân số không bằng nhau

Bài 1:
a: 6/9=2/3
6/24=1/4
48/96=1/2
42/98=3/7
b: 24/36=2/3
18/30=3/5
15/120=1/8
80/240=1/3
c: 5/25=1/5
75/100=3/4
64/720=4/45
16/1000=2/125
Bài 2:
Các phân số bằng 2/3 là 34/51; 20/30; 84/126
Bài 1 :
a) 6/9 = 2/3 ; 6/24 = 1/4 ; 48/96 = 1/2 ; 42/98 = 3/7
b) 24/36 = 2/3 ; 18/30 = 3/5 ; 15/120 = 1/8 ; 80 / 240 = 1/3
c) 5 / 25 = 1/5 ; 75/100=3/4 ; 64/720=4/45 ; 16/1000=2/125
Bài 2 :
Các phân số bằng 2/3 là :
\(\text{34/51; 20/30; 84/126}\)

\(\frac{1}{5}=\frac{1.3}{5.3}=\frac{3}{15}\)
\(\frac{-10}{55}=\frac{-10\div5}{55\div5}=\frac{-2}{11}\)
Vậy ba cặp số phân số bằng nhau sau khi sử dụng tính chất cơ bản
2 .
\(\frac{-12}{-3}=\frac{-12:3}{-3:3}=\frac{-4}{-1};\frac{7}{-35}=\frac{7:7}{-35:7}=\frac{1}{-5};\frac{-9}{27}=\frac{-9:9}{27:9}=\frac{-1}{3}\)
3 .
\(15min=\frac{1}{4}\)giờ
\(90min=\frac{3}{2}\)giờ

Giải thích: Các phân số đã cho có mẫu dương và các mẫu đó lần lượt là 8 = 23, 5, 20 = 22.5, 125 = 53 đều không chứa thừa số nguyên tố nào khác 2 và 5 nên chúng được viết dưới dạng số thập phân hữu hạn.
3/8 = 0,375 ; −7/5 = -1,4; 13/20 = 0,65 ; −13/125 = -0,104
b. Các phân số đã cho có mẫu dương và các mẫu đó lần lượt là 12=22.3, 22=2.11, 35=7.5, 65 = 5.13 đều có chứa thừa số nguyên tố khác 2 và 5 nên chúng được viết dưới dạng số thập phân vô hạn tuần hoàn
ta được : \(\frac{5}{12}=0.41\left(6\right);\frac{29}{22}=1.3\left(18\right);\frac{27}{35}=0.7;\frac{51}{65}=0.8\)

Ta rút gọn các phân số về dạng tối giản:
Do vậy ta có:
Phân số 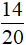
Ta rút gọn các phân số về dạng tối giản:
Do vậy ta có:
Phân số 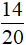

Phân số hữu hạn:
5/8 =0,265vì 8=2^3
-3/20=-0,15 vì 2^.5
14/25=0,56 vì 25=5^2
Phấn số thập phân vô hạn tuần hoàn là:
4/11=0,(36) vì 11=11
15/22 =0,68(18)vì 22=2.11
-7/12=-0,58(3) vì 12=2^2.3

a) Ta có: \( - 0,625 = \frac{{ - 625}}{{1000}}= \frac{{ - 625:125}}{{1000:125}} = \frac{{ - 5}}{8}\)
\(\begin{array}{l}\frac{5}{{ - 8}} = \frac{{ - 5}}{8};\\\frac{{10}}{{16}} = \frac{{10:2}}{{16:2}} = \frac{5}{8};\\\frac{{20}}{{ - 32}} = \frac{{20:( - 4)}}{{( - 32):( - 4)}} = \frac{{ - 5}}{8};\\\frac{{ - 10}}{{16}} = \frac{{( - 10):2}}{{16:2}} = \frac{{ - 5}}{8};\\\frac{{ - 25}}{{40}} = \frac{{( - 25):5}}{{40:5}} = \frac{{ - 5}}{8};\\\frac{{35}}{{ - 48}}\end{array}\)
Vậy các phân số biểu diễn số hữu tỉ -0,625 là:
\(\frac{5}{{ - 8}};\frac{{20}}{{ - 32}};\frac{{ - 10}}{{16}};\frac{{ - 25}}{{40}}\)
b) Ta có: \( - 0,625 = \frac{{ -5}}{{8}}\) nên ta biểu diễn số hữu tỉ \(\frac{{ -5}}{{8}}\) trên trục số.
Chia đoạn thẳng đơn vị thành 8 phần bằng nhau, lấy một đoạn làm đơn vị mới, đơn vị mới bằng \(\frac{1}{8}\) đơn vị cũ.
Lấy một điểm nằm trước O và cách O một đoạn bằng 5 đơn vị mới. Điểm đó biểu diễn số hữu tỉ \(\frac{{ -5}}{{8}}\)

24/30
16/10