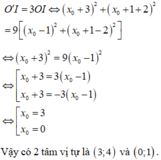Cho hai đường tròn (0) (0') cắt nhau tại hai điểmA và B. các đường thẳng AO,AO cắt đường tròn (0) lần lượt tại các điểm thứ haiC,D và cắt đường tròn(0') tại điểm thứ hai E,F a. Chứng minh B,F,C thẳng hàng
b.Chứng minh AB,CD,FE đồng quy
c.Chứng minh tứ giác CDEF nội tiếp
d.Chứng minh A là tâm đường tròn nội tiếp tam giácBDE
e.MN là một tiếp tuyến chung của(0) và (0') (M,N là tiếp diễn) chứng minh AB đi qua chúng điểm của MN
f.Tìm điều kiện để DE là tiếp tuyến chung của các đường tròn (0) ,(0').
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tọa độ giao điểm là nghiệm của hệ phương trình
x 2 + y 2 − 6 x − 4 y + 9 = 0 x 2 + y 2 − 2 x − 8 y + 13 = 0 ⇔ x 2 + y 2 − 6 x − 4 y + 9 = 0 − 4 x + 4 y − 4 = 0 ⇔ x 2 + y 2 − 6 x − 4 y + 9 = 0 ( 1 ) x − y + 1 = 0 ( 2 )
Từ (2) suy ra: y = x+ 1 thay vào (1) ta được:
x 2 + ( x + 1 ) 2 - 6 x – 4 ( x + 1 ) + 9 = 0 x 2 + x 2 + 2 x + 1 - 6 x - 4 x – 4 + 9 = 0
2 x 2 – 8 x + 6 = 0
Vậy 2 đường tròn đã cho cắt nhau tại 2 điểm là (1; 2) và (3;4).
ĐÁP ÁN B

Đáp án A
Đường tròn C có tâm K 1 ; 2 , bán kính R = 1 + 4 − 4 = 1 .
Đường tròn C ' có tâm K ' − 3 ; − 2 , bán kính R ' = 9 + 4 − 4 = 3.
Giả sử V 1 ; k C = C '
khi đó k = R ' R ⇒ k = 3 ⇔ k = ± 3
Với k = 3 ⇒ I K ' → = 3 I K → ⇒ − 3 − x 1 = 3 1 − x 1 − 2 − y 1 = 3 2 − y 1 ⇒ I 3 ; 4
Với k = − 3 ⇒ I K ' → = − 3 I K → ⇒ − 3 − x 1 = − 3 1 − x 1 − 2 − y 1 = − 3 2 − y 1 ⇒ I 0 ; 1

Đáp án D
Gọi d là đường thẳng qua M có véc tơ chỉ phương:
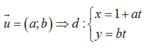
- Đường tròn (C1) tâm I1 (1;1) và R1= 1
Đường tròn (C2) : tâm I2( -2;0) và R2= 3
- Nếu d cắt (C1) tại A :
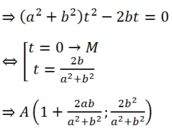
- Nếu d cắt (C2) tại B:
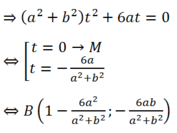
- Theo giả thiết: MA= 2 MB nên MA2= 4 MB2 (*)
- Ta có :
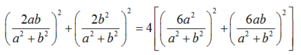
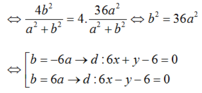

ĐÁP ÁN C
Ta có: 6 2 = − 3 − 1 ≠ 4 3 nên d1 // d2.
Ta có: d 2 : 2 x − y + 3 = 0 ⇔ 6 x − 3 y + 9 = 0
Do d1 // d2. nên khoảng cách hai đường thẳng d1và d2 chính là đường kính của đường tròn.
Suy ra, bán kính đường tròn tiếp xúc với hai đường thẳng d1;d2 là
R = 1 2 d d 1 , d 2 = 1 2 9 − 4 6 2 + − 3 2 = 5 6

Do tâm nằm trên đường thẳng ∆: x + 2y – 5 = 0 nên tâm I(5 – 2y; y). Mà đường tròn tiếp xúc với hai đường thẳng d 1 : 3 x − y + 5 = 0 v à d 2 : x + 3 y − 13 = 0 nên có bán kính R = d I ; d 1 = d I ; d 2
⇒ 3 ( 5 − 2 y ) − y + 5 3 2 + ( − 1 ) 2 = 5 − 2 y + 3 y − 13 1 2 + 3 2
⇒ 20 − 7 y 10 = − 8 + y 10 ⇔ 20 − 7 y = − 8 + y ⇔ 400 − 280 y + 49 y 2 = 64 − 16 y + y 2 ⇔ 48 y 2 − 264 y + 336 = 0 ⇔ y = 2 y = 7 2
Tương ứng ta có hai bán kính của (C) là R 1 = 6 10 , R 2 = 9 2 10
Đáp án là D.

1: sđ cung DE=50 độ
=>góc DOE=50 độ
=>góc DCE=50/2=25 độ; góc BOE=90-50=40 độ
2: Xét (O) có
ΔCED nội tiếp
CD là đường kính
=>ΔCED vuông tại E
Xét tứ giác IODE có
góc IOD+góc IED=180 độ
=>IODE là tứ giác nội tiếp