Cho hàm số: \(y=-\dfrac{1}{2}x^2\).Khảo sát và vẽ đồ thị (P) của hàm số trên
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
BC
2
TL
Trịnh Long
CTVVIP
4 tháng 2 2022
- Tập xác định : D = R
- Hàm số trên là hàm nghịch biến khi x > 0 và đồng biến khi x < 0
Bảng giá trị :
x -4 -2 0 2 4
y -8 -2 0 -2 -8
CM
5 tháng 3 2018
Với m = 2 ta có hàm số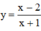 
- Tập xác định : D = R\{-1}.
- Sự biến thiên :
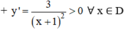
⇒ Hàm số đồng biến trên (-∞ ; -1) và (-1 ; +∞).
+ Cực trị : hàm số không có cực trị
+ Tiệm cận :
⇒ y = 1 là tiệm cận ngang của đồ thị hàm số
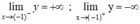
⇒ x = -1 là tiệm cận ngang của đồ thị hàm số.
+ Bảng biến thiên :
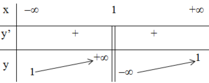
- Đồ thị :
26 tháng 2 2021
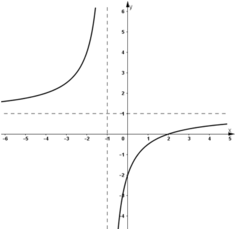
Câu 2:
a) Để đồ thị hàm số \(y=\left(m+1\right)x^2\) đi qua điểm A(1;2) thì
Thay x=1 và y=2 vào hàm số \(y=\left(m+1\right)x^2\), ta được:
m+1=2
hay m=1
Vậy: m=1
PT
1
CM
23 tháng 5 2019
Tập xác định: D = R
y′=0 ⇔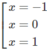 
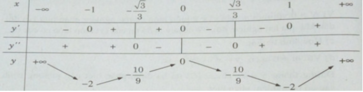
Hàm số đồng biến trên mỗi khoảng (-1; 0) và (1; + ∞ )
Hàm số nghịch biến trên mỗi khoảng (− ∞ ; −1); (0; 1)
Hàm số đạt cực đại tại x = 0; y CĐ = 0
Hàm số đạt cực tiểu tại x = 1 hoặc x = -1; y CT = −2
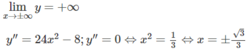
Đồ thị có hai điểm uốn:
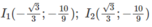
Bảng biến thiên:
Đồ thị:
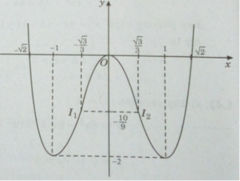
Đồ thị cắt trục hoành tại
Tập xác định : R
Chiều biến thiên : hàm số đồng biến trên \(\left(-\infty;0\right)\)
hàm số nghịch biến trên \(\left(0;+\infty\right)\)
Lập bảng giá trị để vẽ đồ thị