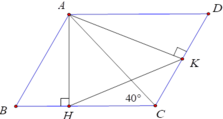
Cho tam giác nhọn ABC có góc C = 40 độ. Vẽ hình bình hành ABCD. Gọi AH, AK theo thứ tự là các đường cao của các tam giác ABC, ACD
a) Chứng minh rằng tam giác AKH đồng dạng với tam giác BCA
b) Tính số đo góc AKH
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì AD.AH = AB.AK ( = S A B C D ) nên A H A K = A B A D = A B B C
Ta lại có AB // CD (vì ABCD là hình bình hành) mà AK ⊥ DC => AK ⊥ AB
=> BAK = 90 ∘ .
Từ đó góc HAK = ABC (cùng phụ với BAH)
Nên ΔAKH ~ ΔBCA (c.g.c) ⇒ A K H ^ = A C B ^ = 40 ∘
Đáp án: B

tự kẻ hình ná
trong tam giác AHC có
AK=KH
HN=CN
=> KN là đtb=> KN//AC và KN=AC/2
tương tự, ta có MK//AB và MK=AB/2
MN//BC và MN=BC/2
Xét tam giác ABC và tam giác KMN có
KN/AC=MN/BC=MK/AB(=1/2) (cũng là tỉ số đồng dạng của 2 tam giác)
=> tam giác ABC đồng dạng với tam giác KMN(ccc)

a)
Xét \(\Delta ABC\)và \(\Delta HBA\) có:
\(\widehat{A}=\widehat{H}=90^o\)
\(\widehat{B}\)là góc chung
\(\Rightarrow\Delta ABC\)đồng dạng với \(\Delta HBA\)
\(\RightarrowĐpcm\)
b)
Xét \(\Delta ABC\) và \(\Delta HAC\) có:
\(\widehat{A}=\widehat{H}=90^o\)
\(\widehat{C}\)là góc chung
\(\Rightarrow\Delta ABC\)đồng dạng với \(\Delta HAC\)
\(\Rightarrow\Delta HBA\)đồng dạng với \(\Delta HAC\) (bắc cầu)
Vì \(\Delta HBA\)đồng dạng với \(\Delta HAC\)
\(\Rightarrow\frac{AH}{HC}=\frac{HB}{AH}\Rightarrow AH^2=HB.HC\Rightarrowđpcm\)
a) - Ta có: SABCD=AH.BC=AK.AB.
=>\(\dfrac{AH}{AK}=\dfrac{AB}{BC}\)
- Ta có: \(\widehat{ABC}+\widehat{BAD}=180^0\) (AD//BC).
=>\(\widehat{ABC}+\widehat{BAH}+\widehat{HAK}+\widehat{KAD}=180^0\)
=>\(90^0+\widehat{HAK}+\widehat{KAD}=180^0\)
=>\(\widehat{HAK}+\widehat{KAD}=90^0\) mà \(\widehat{KAD}+\widehat{ADK}=90^0\) (tam giác ADK vuông tại K) nên \(\widehat{HAK}=\widehat{ADK}\) mà \(\widehat{ADK}=\widehat{ABC}\) (ABCD là hình bình hành) nên\(\widehat{HAK}=\widehat{ABC}\)
- Xét tam giác AKH và tam giác BCA có:
\(\dfrac{AH}{AK}=\dfrac{AB}{BC}\) (cmt)
\(\widehat{HAK}=\widehat{ABC}\) (cmt)
=> Tam giác AKH ∼ Tam giác BCA (c-g-c).
b) - Ta có: Tam giác AKH ∼ Tam giác BCA (cmt) nên:
\(\widehat{AKH}=\widehat{ACB}=40^0\) (2 góc tương ứng)