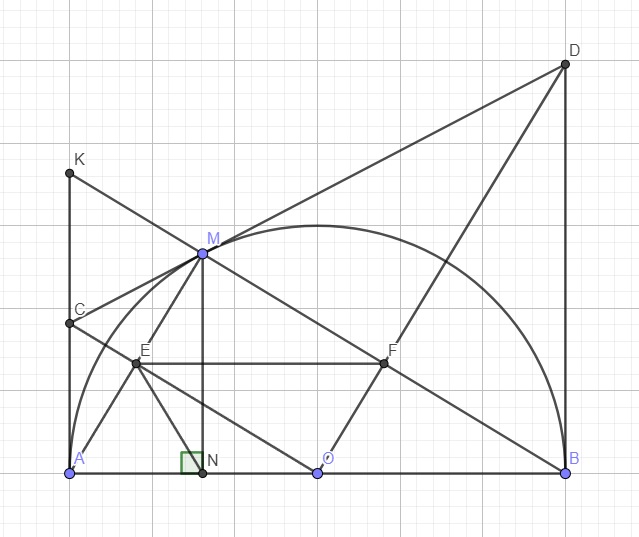
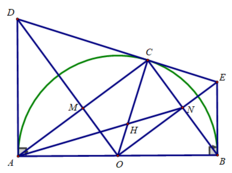
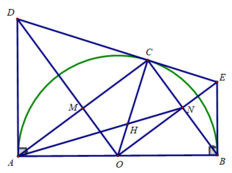
Cho nửa đường tròn tâm O đường kính AB. Trên nửa mặt phẳng bờ AB chứa nửa đường tròn vẽ hai tiếp tuyến Ax, By với nửa O .lấy điểm C trên nửa đường tròn, kẻ tiếp tuyến tại C cắt Ax tại E, Cắt By tại F, BC cắt AE tại D.
a) chứng minh AD2 = DB.DC
b) Chứng minh E là trung điểm của AD


a: Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
Xét ΔADB vuông tại A có AC là đường cao
nên \(AD^2=DB\cdot DC\)
b: Xét (O) có
EC là tiếp tuyến
EA là tiếp tuyến
Do đó: EC=EA
=>ΔECA cân tại C
=>góc ECA=góc EAC
\(\Leftrightarrow90^0-\widehat{ECA}=90^0-\widehat{EAC}\)
hay \(\widehat{EDC}=\widehat{ECD}\)
=>ΔECD cân tại E
=>ED=EC
mà EC=EA
nên EA=ED
hay E là trung điểm của AD
có hình không bạn