cho hình vẽ bên chứng minh tam giác abc bằng tam giác adc và ad=ab
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔADB và ΔADC có
AB=AC
AD chung
BD=CD
Do đó: ΔADB=ΔADC
b: Ta có: ΔABD=ΔACD
=>\(\widehat{BAD}=\widehat{CAD}\)
=>AD là phân giác của góc BAC
c: Xét ΔADM vuông tại M và ΔADN vuông tại N có
AD chung
\(\widehat{DAM}=\widehat{DAN}\)
Do đó: ΔADM=ΔADN
=>AM=AN
Xét ΔABC có \(\dfrac{AM}{AB}=\dfrac{AN}{AC}\)
nên MN//BC

Lười đánh máy thật sự:vvv
a) Xét ∆ABD và ∆AED:
AD: cạnh chung
AB=AE(gt)
\(\widehat{BAD}=\widehat{CAD}\) (AD là phân giác góc BAC)
=> ∆ABD=∆AED (c.g.c)
=> BD=DC
b) Theo câu a: ∆ABD=∆AED
=> \(\widehat{ABD}=\widehat{AED}\)
Ta có: \(\left\{{}\begin{matrix}\widehat{ABD}+\widehat{DBK}=180^o\\\widehat{AED}+\widehat{DEC}=180^o\end{matrix}\right.\)
\(\Rightarrow\widehat{DBK}=\widehat{DEC}\)
Xét ∆DBK và ∆DEC:
BD=ED(cm ở a)
\(\widehat{DBK}=\widehat{DEC}\left(cmt\right)\)
\(\widehat{BDK}=\widehat{EDC}\) ( 2 góc đối đỉnh)
=> ∆DBK=∆DEC (g.c.g)
c) Gọi giao điểm của AD và BE là I
Xét ∆BAI và ∆EAI:
AB=AE(gt)
\(\widehat{BAI}=\widehat{EAI}\left(gt\right)\)
AI: cạnh chung
=> ∆BAI=∆EAI (c.g.c)
=> \(\left\{{}\begin{matrix}BI=EI\left(1\right)\\\widehat{AIB}=\widehat{AIE}\end{matrix}\right.\)
Mà \(\widehat{AIB}+\widehat{AIE}=180^o\) (2 góc kề bù)
=> \(\widehat{AIB}=\widehat{AIE}=90^o\left(2\right)\)
Từ (1) và (2) suy ra AD là trung trực của BE.
a) Xét ΔABD và ΔAED có
AB=AE(gt)
\(\widehat{BAD}=\widehat{EAD}\)(AD là tia phân giác của \(\widehat{BAE}\))
AE chung
Do đó: ΔABD=ΔAED(c-g-c)
Suy ra: BD=ED(hai cạnh tương ứng)

a: Xét ΔADC vuông tại A và ΔHAC vuông tại H có
góc ACD chung
=>ΔADC đồng dạng với ΔHAC
b: S ACD=1/2*AC*AD=1/2*AH*CD
=>AC*AD=AH*CD
c: CD=căn 12^2+16^2=20cm
HD=12^2/20=144/20=7,2cm
HC=20-7,2=12,8cm

a. Diện tích hình thang ABCD là :
(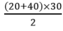 =900
(
c
m
2
)
=900
(
c
m
2
)
Diện tích tam giác ADC là :
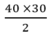 =600
(
c
m
2
)
=600
(
c
m
2
)
Diện tích tam giác ABC là :
900 – 600 = 300 ( c m 2 )
b. Tỉ số phần trăm của diện tích tam giác ABC và hình tam giác ADC là :
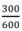 ×100 = 50%
×100 = 50%
Đáp số:
a. Diện tích tam giác ABC : 300 ( c m 2 )
Diện tích tam giác ADC : 600 ( c m 2 )
b. %SABC = 50%
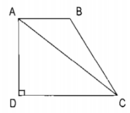
a: Xét ΔABC vuông tại B và ΔADC vuông tại D có
CA chung
\(\widehat{BCA}=\widehat{DCA}\)
Do đó: ΔABC=ΔADC
Suy ra: AB=AD
xét 2 tam giác có
góc ACB = góc ACB
AC cạnh chung
vậy 2 tam giác vuông bằng nhau
=>AB=AD ( 2 cạnh tương ứng)