Bài toán 1: Cho tam giác ABC, biết ![]()
![]()
a) So sánh các cạnh của tam giác
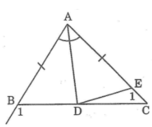
b) Tia phân giác của góc A cắt BC ở D. So sánh độ dài các đoạn BD và CD.
Bài toán 2: Cho tam giác ABC cân ở A có chu vi bằng 16cm, cạnh đáy BC = 4cm. So sánh các góc của tam giác ABC.
Bài toán 3: Cho tam giác ABC, biết ![]() So sánh các cạnh của tam giác.
So sánh các cạnh của tam giác.
Bài toán 4: Cho tam giác ABC, góc A là góc tù. Trên cạnh AC lấy hai điểm D và E (D nằm giữa A và E). Chứng minh rằng ![]()
Bài toán 5: Cho tam giác ABC CÓ ![]()
a) So sánh độ dài các cạnh AB và AC
b) Gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho ![]() Chứng minh
Chứng minh ![]() .
.
Bài toán 6: Tam giác ABC có ![]() Tia phân giác của góc A cắt BC ở D. Chứng minh rằng điểm D nằm giữa hai điểm B và m (M là trung điểm của BC).
Tia phân giác của góc A cắt BC ở D. Chứng minh rằng điểm D nằm giữa hai điểm B và m (M là trung điểm của BC).
Bài toán 7: Tam giác ABC cân tại A. Kẻ tia Bx nằm giữa hai tia BA và BC. Trên tia Bx lấy điểm D nằm ngoài tam giác ABC. Chứng minh rằng ![]()
Bài toán 8: Cho tam giác ABC cân ở A, kẻ ![]() Trên các đoạn thẳng HD và HC, lấy các điểm D và E sao cho
Trên các đoạn thẳng HD và HC, lấy các điểm D và E sao cho ![]() So sánh độ dài AD, AE bằng cách xét hai hình chiếu.
So sánh độ dài AD, AE bằng cách xét hai hình chiếu.
Bài toán 9: Cho tam giác ABC có ![]() và
và ![]() là các góc nhọn. Gọi D là điểm bất kfi thuộc cnahj BC, gọi H và K là chân các đường vuông góc kẻ từ B và C đến đường thẳng AD.
là các góc nhọn. Gọi D là điểm bất kfi thuộc cnahj BC, gọi H và K là chân các đường vuông góc kẻ từ B và C đến đường thẳng AD.
a) So sánh các độ dài BH và BD. Có khi nào BH bằng BD không?
b) So sánh tổng độ dài BH + CK với BC.
Bài toán 10: Cho tam giác ABC cân ở A. Trên cạnh BC lấy điểm D và E sao cho ![]() Gọi M là trung điểm của DE.
Gọi M là trung điểm của DE.
a) Chứng minh rằng ![]()
b) So sánh độ dài AB, AD, AE, AC.
Bài toán 11: Cho tam giác ABC ![]() Gọi M là một điểm nằm giữa B và C. Gọi E và F là hình chiếu của B và C xuống đường thẳng AM. So sánh tổng
Gọi M là một điểm nằm giữa B và C. Gọi E và F là hình chiếu của B và C xuống đường thẳng AM. So sánh tổng ![]() với BC
với BC

Bài toán 2: Cho tam giác ABC cân ở A có chu vi bằng 16cm, cạnh đáy BC = 4cm. So sánh các góc của tam giác ABC.
Tam giác ABC cân tại A (gt). => Góc B = Góc C (Tính chất tam giác cân).
Ta có: Tam giác ABC cân ở A có chu vi bằng 16cm, cạnh đáy BC = 4cm (gt).
=> AB = AC = (16 - 4) : 2 = 6 (cm).
Xét tam giác ABC cân tại A:
Ta có: AB > BC (AB = 6 cm; BC = 4cm).
=> Góc C > Góc A.
Vậy trong tam giác ABC có Góc B = Góc C > Góc A.