cho tam giác BC. Vẽ hai đường trung trực của AB và AC. Hai đường trung trực cắt nhau tại O.
Chứng minh rằng O nằm trên đường trung trực của BC.
Chứng minh:OA=OB=OC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tự vẽ hình nhé !
Gọi trung trực của AB cắt AB tại M ,trung trực của BC cắt BC tại N nên OM _|_ AB ; ON _|_ BC ; MA = MB ; NB = NC
=>\(\Delta OMB,\Delta OMA\)vuông tại M có chung cạnh OM ; MB = MA
=>\(\Delta OMB=\Delta OMA\) (2 cạnh góc vuông) => OB = OA (2 cạnh tương ứng) (1);
\(\Delta ONB,\Delta ONC\)vuông tại N có chung cạnh ON ; NB = NC
\(\Rightarrow\Delta ONB=\Delta ONC\)(2 cạnh góc vuông) => OB = OC (2 cạnh tương ứng) (2)
Từ (1),(2),ta có OA = OB = OC
P/S : Kết luận (1) và (2) đều cho thấy : Điểm nằm trên trung trực của 1 đoạn thẳng thì cách đều 2 mút của đoạn đó.Kết luận của bài toán cho thấy : Giao điểm của 2 đường trung trực của tam giác cách đều 3 đỉnh của tam giác nên có thể vẽ được 1 đường tròn đi qua 3 đỉnh tam giác gọi là đường tròn ngoại tiếp của tam giác.Trong bài trên,O là tâm đường tròn ngoại tiếp,OA = OB = OC là các bán kính.
Các tính chất này sẽ được chứng minh trong SGK Toán 7 tập 2

Vì ba đường trung trực của tam giác đồng quy nên D thuộc đường trung trực của cạnh BC. Mặt khác đường trung trực của cạnh BC đi qua trung điểm của BC nên D là trung điểm của cạnh BC.

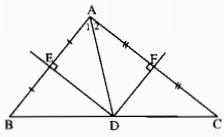
a) Vì ba đường trung trực của tam giác đồng quy nên D thuộc đường trung trực của cạnh BC. Mặt khác đường trung trực của cạnh BC đi qua trung điểm của BC nên D là trung điểm của cạnh BC.
b) Ta có: Tam giác DEA = tam giác DEA (c.g.c) nên góc B = góc A1
<=> góc C = góc A2
=> Góc A = góc A1 + góc A2 = góc B + góc C.

+) Xét tam giác ADE và BDE có:
DE chung
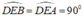
DA = DB ( vì DE là đường trung trực của AB)
Suy ra: ∆ADE = ∆ BDE ( cạnh huyền – cạnh góc vuông).
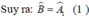
+ Chứng minh tương tự ta có: ∆ADF = ∆ CDF ( cạnh huyền – cạnh góc vuông).
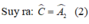
Từ (1) và (2) suy ra: 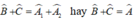

Do O thuộc đường trung trực của MC
\(\Rightarrow MO=OC\) (1)
Do O thuộc đường trung trực của BC
\(\Rightarrow OC=OB\) 2)
Từ (1) và (2) \(\Rightarrow OM=OB\)
Lại có: \(AM=AB\)
\(\Rightarrow AO\) là đường trung trực của BM