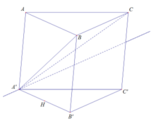
Cho hình lăng trụ A’B’C’.ABC
A) tìm giao tuyến của (AB’C) và (A’B’C’)
B) chứng minh giao tuyến của(ab’c) và (A’BC’) song song (ABC) và song song với (a’b’c) và song song với aa’c’c)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

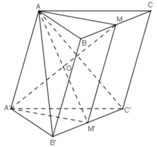
a) Do ABC.A’B’C’ là hình lăng trụ nên ta có: BCC’B’ là hình bình hành
Xét tứ giác BCC’B’ có M và M’ lần lượt là trung điểm của BC và B’C’ nên MM’ là đường trung bình
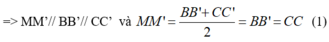
Lại có: AA’// BB’ và AA’= BB’ ( tính chất hình lăng trụ) (2)
Từ (1) và (2) suy ra: MM’// AA’ và MM’ = AA’
=> Tứ giác AMM’A’ là hình bình hành
b) Trong (AMM’A’) gọi O = A’M ∩ AM’, ta có :
Ta có : O ∈ AM’ ⊂ (AB’C’)
⇒ O = A’M ∩ (AB’C’).
c)
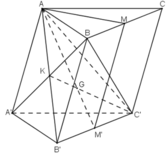
Gọi K = AB’ ∩ BA’, ta có :
K ∈ AB’ ⊂ (AB’C’)
K ∈ BA’ ⊂ (BA’C’)
⇒ K ∈ (AB’C’) ∩ (BA’C’)
Dễ dàng nhận thấy C’ ∈ (AB’C’) ∩ (BA’C’)
⇒ (AB’C’) ∩ (BA’C’) = KC’.
Vậy d cần tìm là đường thẳng KC’
d) Trong mp(AB’C’), gọi C’K ∩ AM’ = G.
Ta có: G ∈ AM’ ⊂ (AM’M)
G ∈ C’K.
⇒ G = (AM’M) ∩ C’K.
+ K = AB’ ∩ A’B là hai đường chéo của hình bình hành ABB’A’
⇒ K là trung điểm AB’.
ΔAB’C’ có G là giao điểm của 2 trung tuyến AM’ và C’K
⇒ G là trọng tâm ΔAB’C’.

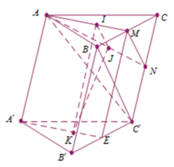
Gọi M, N, E lần lượt là trung điểm của BC, CC′, B′C′.
Suy ra (tính chất trọng tâm tam giác) nên IJ // MN (1).
Trong mặt phẳng (AA′ME) ta có
⇒ IK // ME
mà ME // BB′ nên IK // BB′ (2).
Từ (1) và (2) do (IJK) và (BB′C′) là hai mặt phẳng phân biệt
IJ; IK ∈ (IJK)
Nên IJ // (BB′C′), IK // (BB′C′)
Suy ra (IJK) // (BB′C′)
Đáp án cần chọn là: C

Áp dụng định lý Py-ta-go: Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
Áp dụng định lý 2 đường trung bình của tam giác: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy
Lời giải chi tiết:
Áp dụng định lí Py-ta-go cho ΔABC vuông tại A ta có:
BC2=AB2+AC2⇒BC2=32+42=25⇒BC=5cm
Mà {AE=EB(gt)AF=FC(gt) ⇒EF là đường trung bình của ΔABC (định nghĩa)
⇒EF=12BC=12×5=2,5cm (tính chất đường trung bình của tam giác).

Đáp án B
Xét (A’B’C’) và (A’BC) có:
A’ là điểm chung
B’C’ // BC
giao tuyến của 2 mặt phẳng là đường thẳng d qua A’ song song với B’C’
⇒ d và B’C’ đồng phẳng
Mà d chứa A’
⇒ d thuộc mặt phẳng (A’B’C’)
Mà H ∈ A’B’ ⇒ H ∈ (A’B’C’)
⇒ Mặt phẳng đi qua d và H, cắt tứ diện ABC. A’B’C’ là (A’B’C’)


Vì K là trung điểm BC nên B, K, C thẳng hàng theo thứ tự đó và BK = KC. Do vậy B', K', C' thẳng hàng theo thứ tự đó và B'K' = K'C', tức K' là trung điểm B'C'.
Vì G là trọng tâm tam giác ABC nên A, G, K thẳng hàng theo thứ tự đó và AG = 2GK. Do vậy A, G', K' thẳng hàng theo thứ tự đó và A'G' = 2G'K', tức G là trọng tâm tam giác A'B'C'.
a. Do \(AC||A'C'\Rightarrow\) giao tuyến của (AB'C) và (A'B'C') là đường thẳng qua B' và song song A'C'
Qua B kẻ \(d||A'C'\Rightarrow d=\left(AB'C\right)\cap\left(A'B'C'\right)\)
b. Trong mp (ABB'A'), gọi M là giao điểm AB' và A'B
Trong mp (BCC'B'), gọi N là giao điểm BC' và B'C
\(\Rightarrow MN=\left(AB'C\right)\cap\left(A'BC'\right)\)
Mặt khác do các mặt bên của lăng trụ là các hình bình hành
\(\Rightarrow\) M là trung điểm AB' và A'B, N là trung điểm BC' và B'C
\(\Rightarrow MN||AC\) (đường trung bình)
\(\Rightarrow\left\{{}\begin{matrix}MN||\left(ABC\right)\\MN||\left(AA'C'C\right)\end{matrix}\right.\)
MN song song (A'B'C) là sai, MN chỉ song song (A'B'C')