Một quả bóng m=250g bay tới đập vuông góc vào tường với tốc độ v1=5m/s và bật ngược trở lại với v=3m/s. Độ biến thiên động lượng của vật trong khoảng thời gian đó có độ lớn bằng bao nhiêu?.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải
Chọn chiều dương là chiều chuyển động của quả bóng sau khi đập vào tường
Ta có:
+ Trước khi đập vào tường, động lượng của quả bóng: p 1 = − m v 1 = − 0 , 5.20 = − 10 k g . m / s
+ Sau khi đập vào tường, động lượng của quả bóng: p 2 = m v 2 = 0 , 5.20 = 10 k g . m / s
Độ biến thiên động lượng Δ p = p 2 − p 1 = 10 − − 10 = 20 k g . m / s
Đáp án: C

Chọn C.
+ Biểu diễn véc tơ động lượng lúc trước và lúc sau
+ p → động lượng lúc trước.
+ p ' → động lượng lúc sau.
+ Độ biến thiên động lượng của quả bóng do va chạm
![]()
+ Từ hình biểu diễn véc tơ ta có độ lớn:
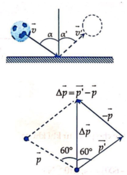
∆p = p’ = p = m.v = 0,2.25 = 5 kg.m/s.
(vì tam giác tạo bởi 3 cạnh này là tam giác cân có 1 góc 60° là tam giác đều).

Chọn C.
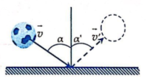
+ Biểu diễn véc tơ động lượng lúc trước và lúc sau
+ p ⇀ động lượng lúc trước.
+ p ' ⇀ động lượng lúc sau.
+ Độ biến thiên động lượng của quả bóng do va chạm
δ p ⇀ = p ' ⇀ - p ⇀ = p ' ⇀ + - p ⇀
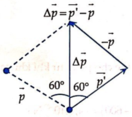
+ Từ hình biểu diễn véc tơ ta có độ lớn:
∆ p = p’ = p = m.v = 0,2.25 = 5 kg.m/s.
(vì tam giác tạo bởi 3 cạnh này là tam giác cân có 1 góc 60° là tam giác đều).

Chọn đáp án C
Hướng dẫn:
Áp dụng công thức về độ biến thiên động lượng:
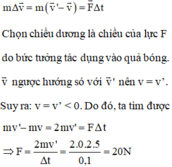

Chọn A.
Chọn chiều dương là chiều chuyển động của quả bóng sau khi va chạm.
Lực của tường tác dụng lên quả bóng:
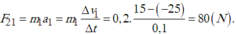
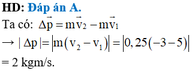
\(m=250g=0,25kg\)
\(v_1=5\)m/s\(;v_2=3\)m/s
Độ biến thiên động lượng vật:
\(\Delta p=m\overrightarrow{v_2}-m\overrightarrow{v_1}\)
Mà bóng bay rồi đập trở lại tường\(\Rightarrow v_2\uparrow\downarrow v_1\)
\(\Rightarrow\Delta p=m\cdot v_2-m\cdot\left(-v_1\right)=0,25\cdot5-0,25\cdot\left(-3\right)=2kg.\)m/s