có hai lô hàng, mỗi lô có 10 sản phẩm. Lô I có 3 sản phẩm loại A. Lô II có 6 sản phẩm loại A.1/ Nếu từ mỗi lô lấy ra 1 sản phẩm. Tính xác suất để hai sản phẩm lấy ra từ 2 lô:a/ có đúng 1 sản phẩm loại Ab/ cùng loại2/ Từ lô I lấy 3 sản phẩm bỏ sang lô II, rối từ lô II lấy ra 1 sản phẩm. Tính xác suất để sản phẩm lấy ra từ lô II là loại...
Đọc tiếp
có hai lô hàng, mỗi lô có 10 sản phẩm. Lô I có 3 sản phẩm loại A. Lô II có 6 sản phẩm loại A.
1/ Nếu từ mỗi lô lấy ra 1 sản phẩm. Tính xác suất để hai sản phẩm lấy ra từ 2 lô:
a/ có đúng 1 sản phẩm loại A
b/ cùng loại
2/ Từ lô I lấy 3 sản phẩm bỏ sang lô II, rối từ lô II lấy ra 1 sản phẩm. Tính xác suất để sản phẩm lấy ra từ lô II là loại A
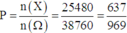
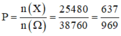
1/
a/ TH1: Lấy 1 sp loại A từ lô I có: \(C^1_3\) (cách)
Lấy 1 sp từ 4 sp còn lại từ lô II có: \(C^1_4\) (cách)
\(\Rightarrow C^1_3.C^1_4\) (cách)
TH2: Lấy 1 sp loại A từ lô II có: \(C^1_6\) (cách)
Lấy 1 sp từ 7 sp còn lại từ lô I có: \(C^1_7\) (cách)
\(\Rightarrow C^1_6.C^1_7\) (cách)
Không gian mẫu: \(n\left(\Omega\right)=C^1_{10}.C^1_{10}\)
\(\Rightarrow p\left(M\right)=\dfrac{C^1_6.C^1_7+C^1_3.C^1_4}{C_{10}^1.C^1_{10}}=0,54\)
b/ TH1: Lấy 1 sp loại A từ lô I: \(C^1_3\) (cách)
Lấy 1 sp loại A từ lô II: \(C^1_6\) (cách)
\(\Rightarrow C^1_3.C^1_6\) (cách)
TH2: Lấy 1 sp từ 7 sp còn lại trong lô I: \(C^1_7\) (cách)
Lấy 1 sp từ 4 sp còn lại trong lô II: \(C^1_4\) (cách)
\(\Rightarrow C^1_7.C^1_4\) (cách)
\(\Rightarrow p\left(O\right)=\dfrac{C_3^1.C_6^1+C^1_7.C^1_4}{C^1_{10}.C^1_{10}}=...\)
Bài 2 mình ko chắc nên ko làm nhé :(
Cho mình hỏi bài tập này với
Một gia đình có 6 con, biết rằng khả năng sinh con trai và con gái độc lập với nhau và có xác suất là 0,5. Một người khách đến thăm thì thấy có 2 con trai đang ở nhà. Tính xác suất gia đình đó có
1. Ba con trai.
2. Tối đa ba con trai