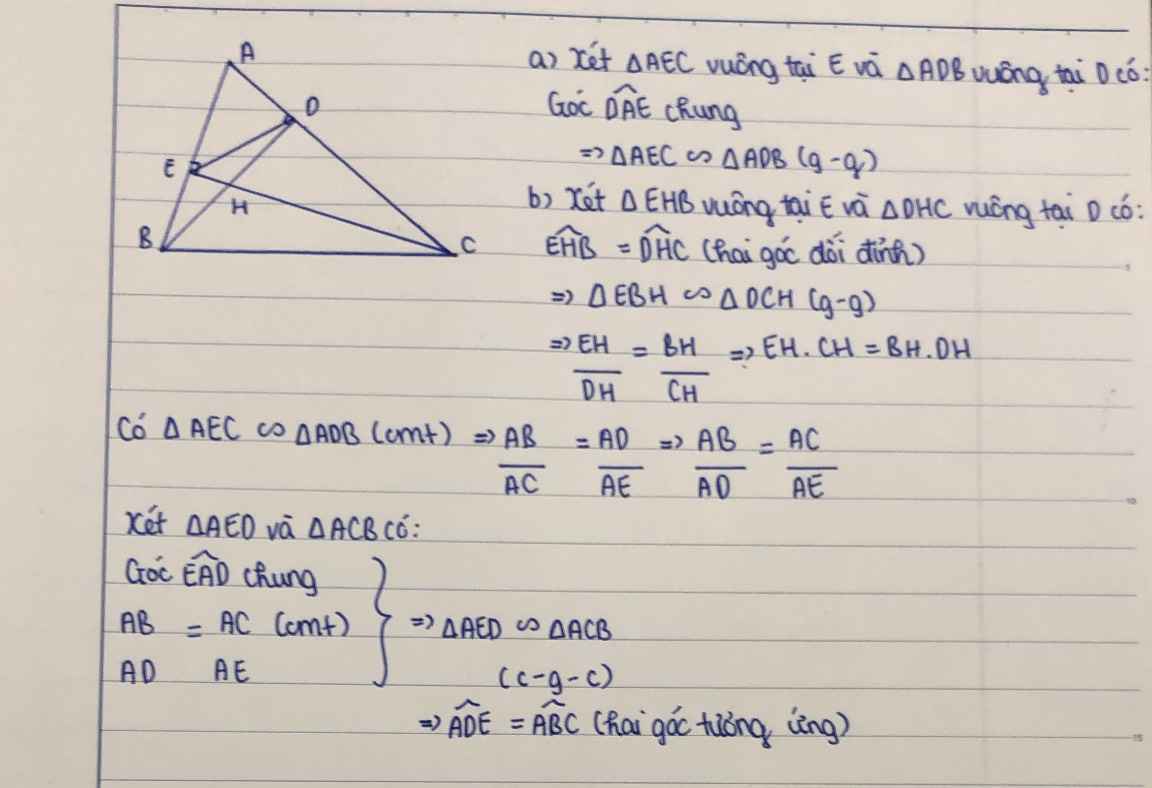cho tam giác ABC AD BK CL là ccas đường cao chứng minh tam giác AKL đồng dangj vs tam giác ABC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 3 2023
a: Xét ΔAHB vuông tại H và ΔCHA vuông tạiH có
góc HAB=góc HCA
=>ΔAHB đồng dạng với ΔCHA
c: BK là phân giác
=>AK/CK=BA/BC
ΔAHC có AD là phân giác
nên DH/CD=AH/AC=BA/BC
=>DH/CD=AK/CK
=>KD//AH
24 tháng 3 2021
a) Xét ΔAHB vuông tại H và ΔCAB vuông tại A có
\(\widehat{CBA}\) chung
Do đó: ΔAHB\(\sim\)ΔCAB(g-g)
9 tháng 5 2022
a, Xét Δ ABD và Δ ABE, có :
\(\widehat{ADB}=\widehat{AEB}=90^o\)
\(\widehat{BAD}=\widehat{BAE}\) (góc chung)
=> Δ ABD ∾ Δ ABE (g.g)
b, Xét Δ EHB và Δ DHC, có :
\(\widehat{EHB}=\widehat{DHC}\) (đối đỉnh)
\(\widehat{HEB}=\widehat{HDC}=90^o\)
=> Δ EHB ∾ Δ DHC (g.g)
=> \(\dfrac{EH}{DH}=\dfrac{HB}{HC}\)
=> \(HB.HD=HC.HE\)
CM
12 tháng 10 2018
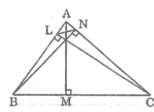
a. Xét hai tam giác BNA và CLA, ta có:
∠ BNA = ∠ CLA = 90 °
góc A chung
Suy ra ∆ BNA đồng dạng ∆ CLA (g.g)
Suy ra: AL/AN = AC/AB ⇒ AL/AC = AN/AB
Xét hai tam giác ABC và ANL, ta có:
AL/AC = AN/AB
góc A chung
Suy ra ∆ ABC đồng dạng ∆ ANL (c.g.c)