Cho đường tròn (O) đường kính AB. Gọi H là điểm nằm giữa O và B. Kể dây CD vuông góc AB tại H. Trên cung nhỏ AC lấy điểm E. Kẻ CK vuông góc AE tại K. Đường thẳng DE cắt CK tại F.
a) T/g AHCK nội tiếp
b) AH.AB=AD^2
c) Tam giác ACF là tam giác cân
ai chỉ em câu b vs ạ

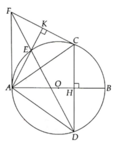
Do AB là đường kính và D thuộc đường tròn
\(\Rightarrow\widehat{ADB}\) là góc nội tiếp chắn nửa đường tròn
\(\Rightarrow\widehat{ADB}=90^0\) hay tam giác ADB vuông tại D
Xét tam với vuông ADB với đường cao DH, áp dụng hệ thức lượng ta có:
\(AD^2=AH.AB\)