Cho tam giác ABC có góc A = 90°, trên cạnh BC lấy điểm E sao cho BE = BA. Tia phân giác của góc B cắt AC ở D. Kéo dài ED cắt tia BA tại K. a) Cho BC = 10 cm, AB = 6cm. Hãy tính AC. b) Chứng minh : DA = DE. c) Chúng minh rằng: tam giác DKC là tam giác cân.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Xét ΔDAB và ΔDEB có
BA=BE(gt)
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
BD chung
Do đó: ΔDAB=ΔDEB(c-g-c)
Suy ra: DA=DE(Hai cạnh tương ứng)

a: \(AC=\sqrt{BC^2-AB^2}=8\left(cm\right)\)
b: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
Suy ra: DA=DE
c: Xét ΔADK vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADK}=\widehat{EDC}\)
DO đó: ΔADK=ΔEDC
Suy ra: DK=DC
hay ΔDKC cân tạiD
tự vẽ hình giúp mình nha ^^
áp dụng định lí py-ta-go vào tam giác vuông ABC
\(\Rightarrow AB^2+AC^2=BC^2\)
\(\Leftrightarrow AC^2=BC^2-AB^2\)
\(\Leftrightarrow AC^2=10^2-6^2=100-36=64\)
\(\Rightarrow AC=\sqrt{64}=8\left(cm\right)\)
b) Xét \(\Delta BADvà\Delta BEDcó\)
BD:chung
\(\widehat{ABD}=\widehat{EBD}\left(gt\right)\)
AB=BE(gt)
\(\Delta BAD=\Delta BED\left(c-g-c\right)\)
=>DA=DE
c)Xét \(\Delta KADvà\Delta CEDcó\)
\(\widehat{KAD}=\widehat{CED}\left(=90^0\right)\)
\(\widehat{KDA}=\widehat{CDE}\) (đối đỉnh)
\(=>\Delta KAD=\Delta CED\left(g-c-g\right)\)
=>DC=DK
=> tam giác KDC cân tại D

a, Xét tg ABD và tg EBD có : AB = EB (gt)
gABD = gEBD (BD là tia phân giác của gABE)
BD chung
=> tgABD = tgEBD (c.g.c)
=> DA = DE ( hai cạnh tương ứng )
b,vì tgABD = tgEBD (cmt)
=>gABD = gAEB=90 độ (hai góc tương ứng)
=>gDAK = gDEC = 90 độ
xét tgAKD và tgEDC có: gDAK = gDEC (cmt)
AD = DE ( cmt)
gADK = gEDC ( hai góc đối đỉnh)
=> tgAKD = tgEDC (g.c.g)
=> DK = DC (hai cạnh tương ứng)
=> tg DKC cân tại D
c,xét tgABC vuông tại A ( góc A = 90độ , theo định lí Pytago ta có
BC^2=AB^2 + AC^2
=>AC^2 = 100- 36=64
=> AC = 8 (cm)
a, xét tam giác ABD và tam giác EBD có : BD chung
BA = BE (Gt)
góc ABD = góc EBD do BD là phân giác của góc ABC (gt)
=> tam giác ABD = tam giác EBD (c-g-c)
=> AD = DE (đn)
b, Xét tam giác DCE và tam giác KDA có : AD = DE (Câu a)
góc KDA = góc CDE (đối đỉnh)
góc CED = góc DAK = 90
=> tam giác CE = KA (đn)
có AB = BE (gt)
AB + KA = BK
BE + EC = BC
=> BC = BK
=> BCK cân tại B (đn)
c, dùng ty ta go thôi

a: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
Suy ra: DA=DE
b: Xét ΔADK vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADK}=\widehat{EDC}\)
Do đó: ΔADK=ΔEDC
Suy ra: DK=DC
hay ΔDKC cân tại D
c: \(AC=\sqrt{BC^2-AB^2}=8\left(cm\right)\)
d: Ta có: DK=DC
mà DC>DE
nên DK>DE

a: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
Suy ra: DA=DE
b: Xét ΔADK vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADK}=\widehat{EDC}\)
Do đó:ΔADK=ΔEDC
Suy ra:DK=DC
hay ΔDKC cân tại D
c: BC=10cm
AB=6cm
=>AC=8cm

a: Xét ΔABD và ΔEBD có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔABD=ΔEBD

a: BC=10cm
b: Xét ΔABD và ΔEBD có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
DO đó; ΔABD=ΔEBD
Suy ra: \(\widehat{BAD}=\widehat{BED}=90^0\)
hay DE\(\perp\)BC
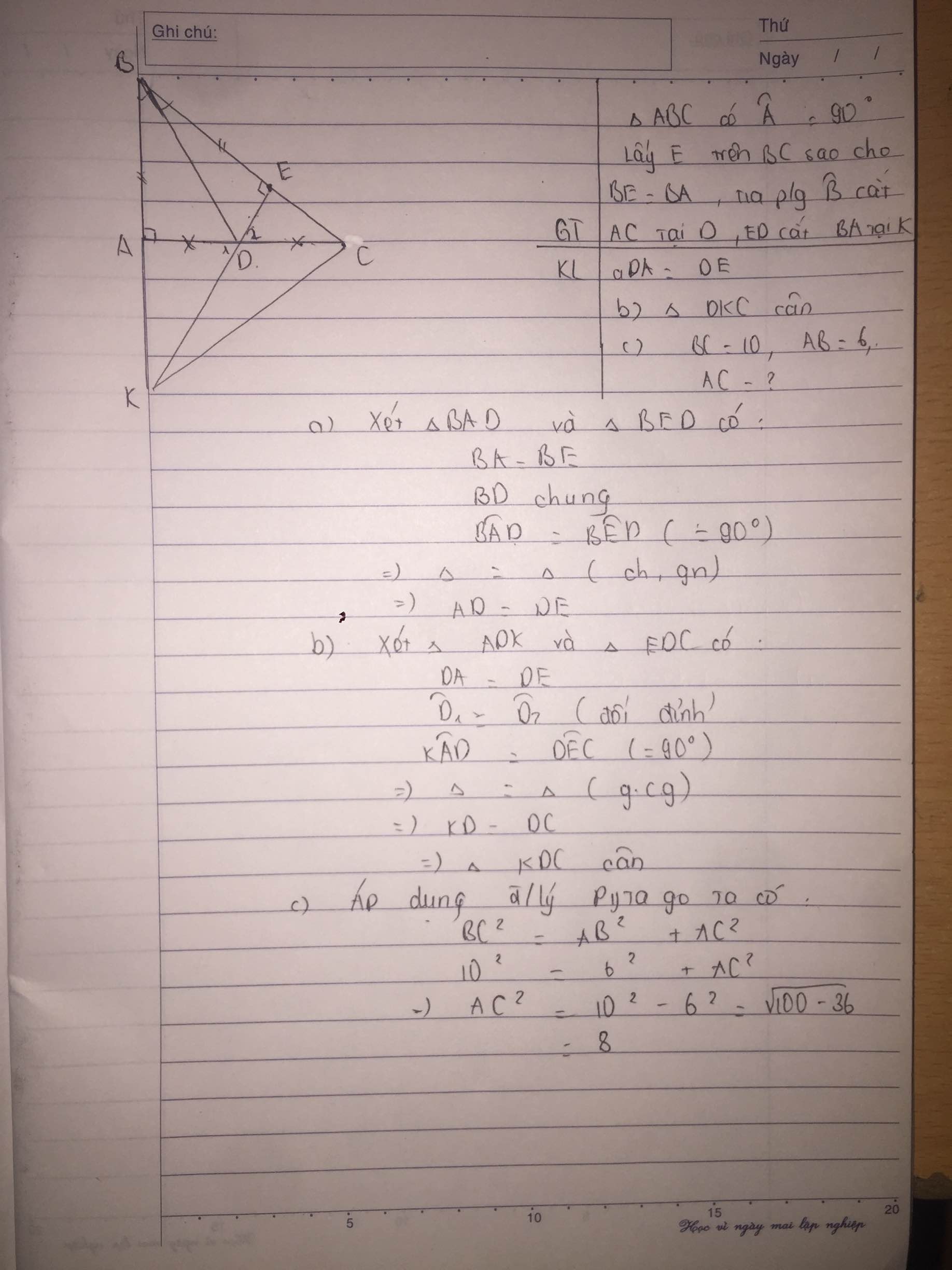
khó đọc đc
a: AC=8cm
b: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
Suy ra: DA=DE
c: Xét ΔADK vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADK}=\widehat{EDC}\)
Do đó: ΔADK=ΔEDC
Suy ra: DK=DC
hay ΔDKC cân tại D